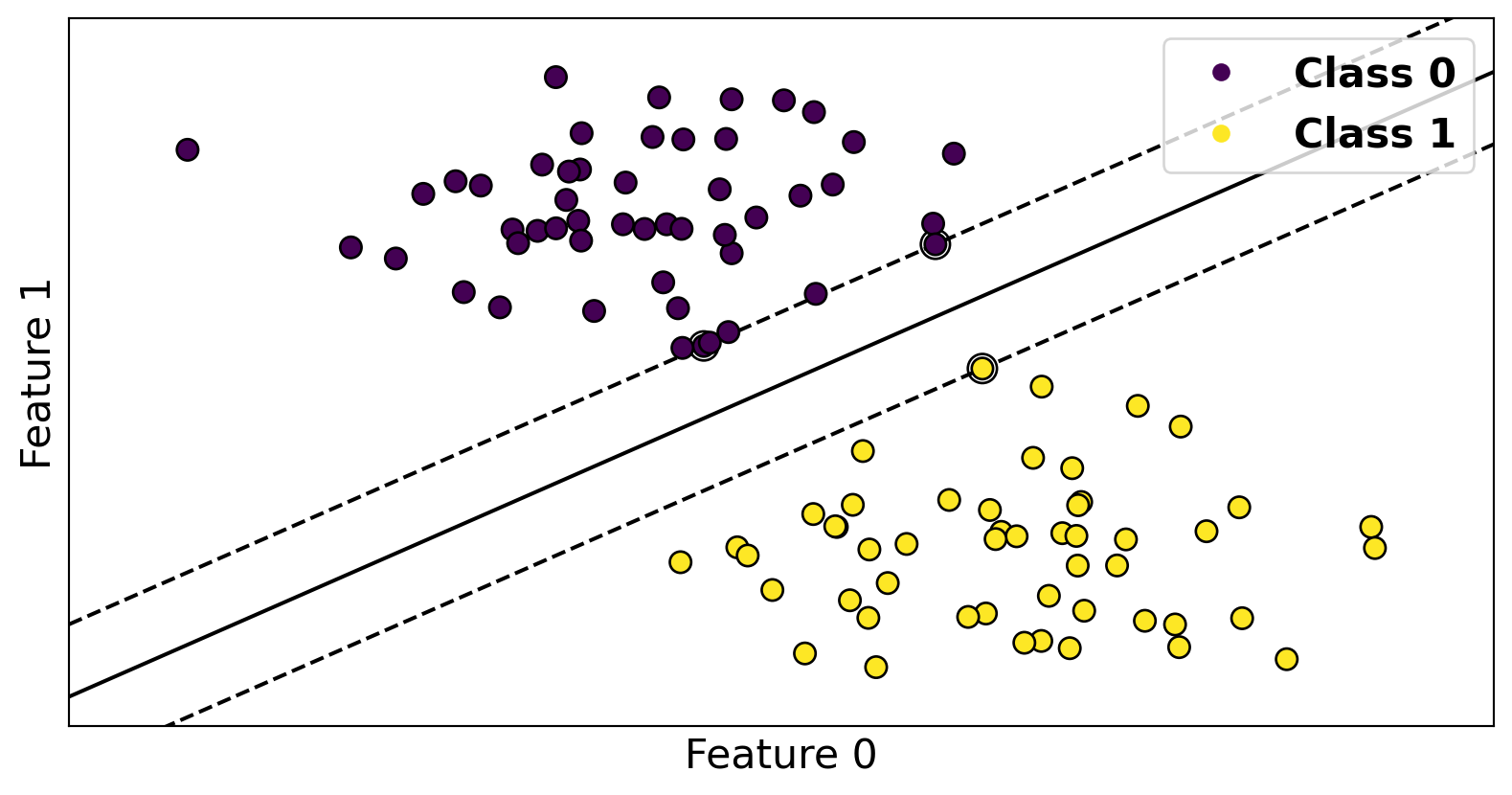
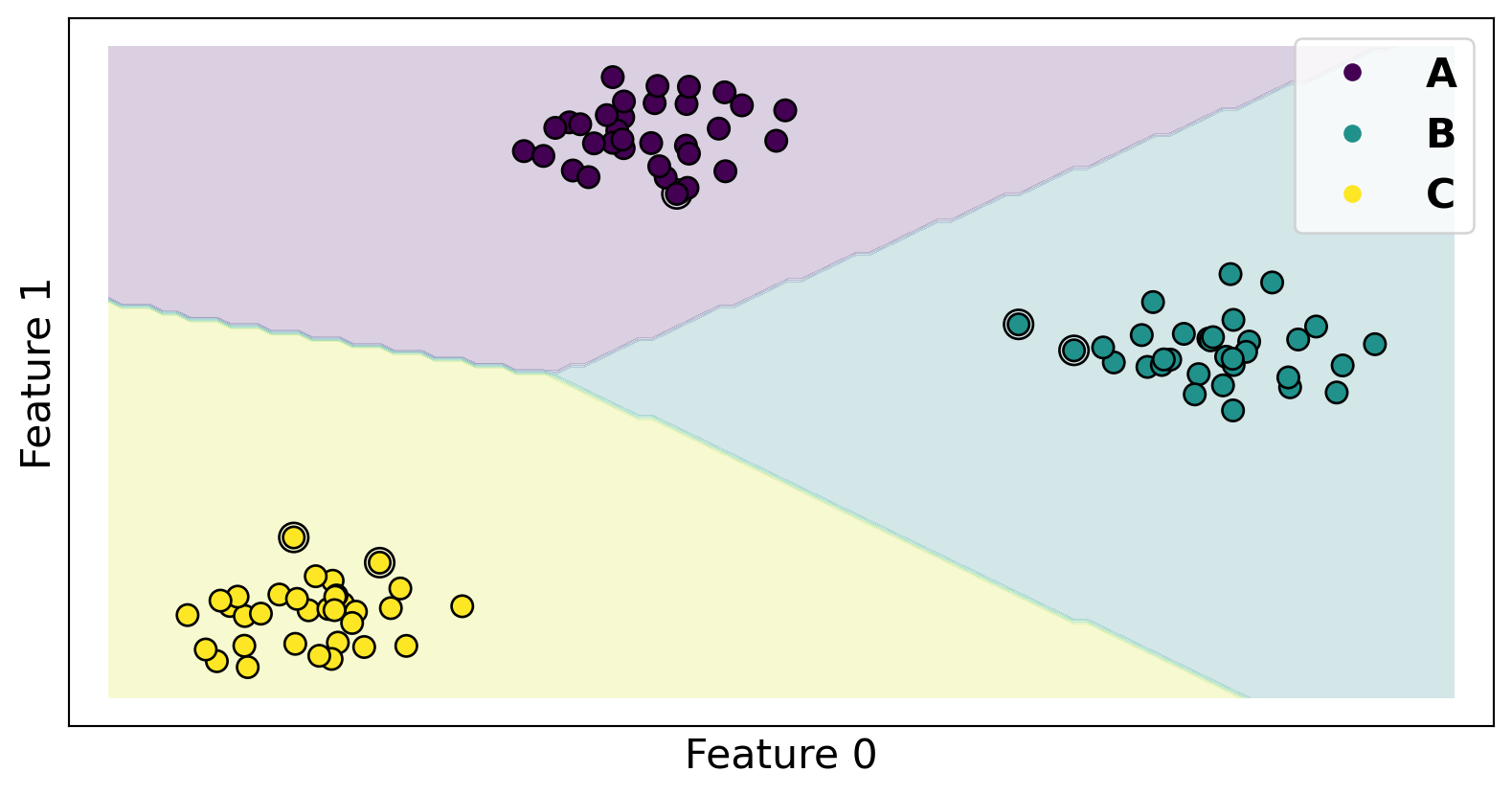
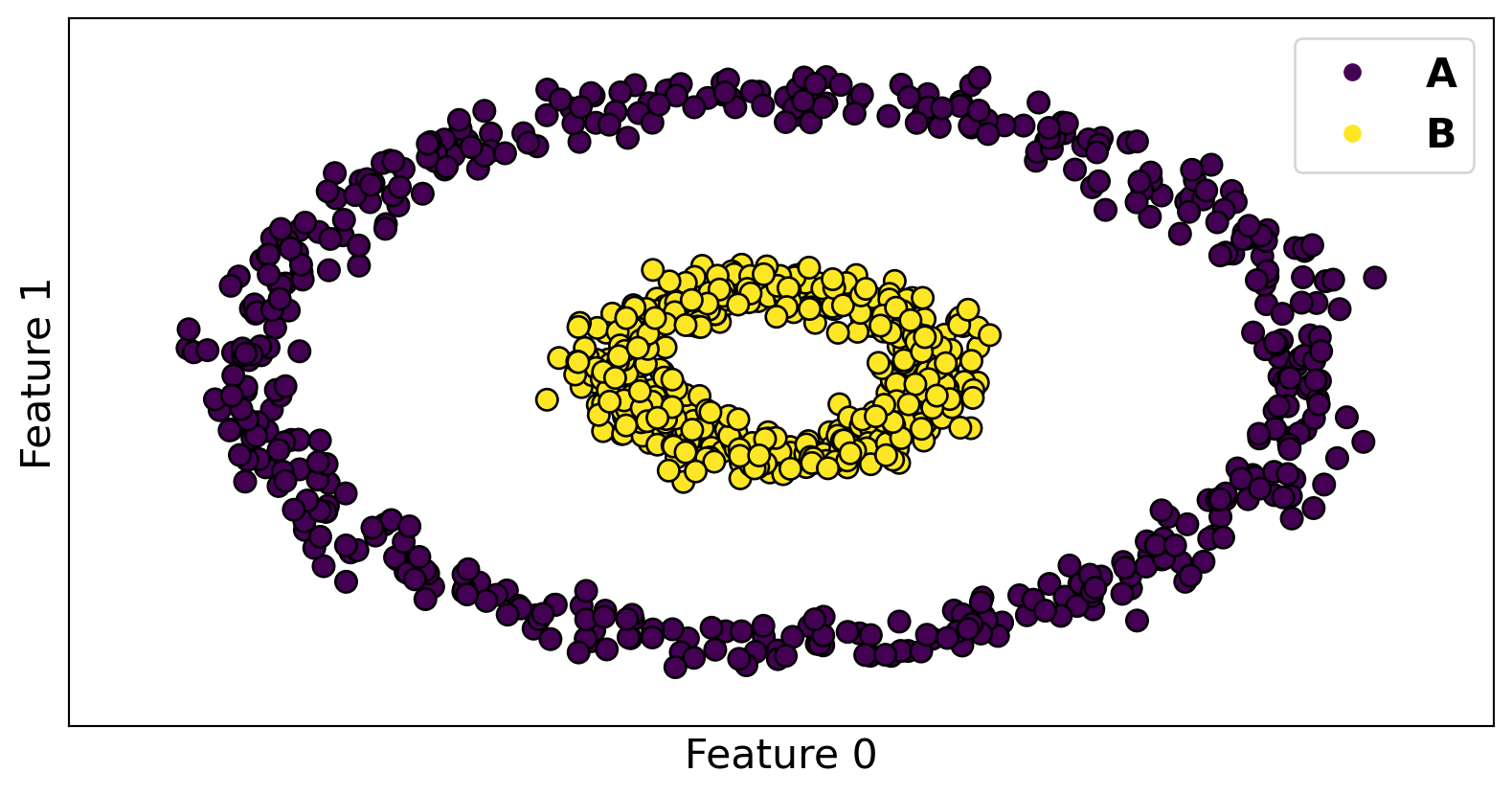
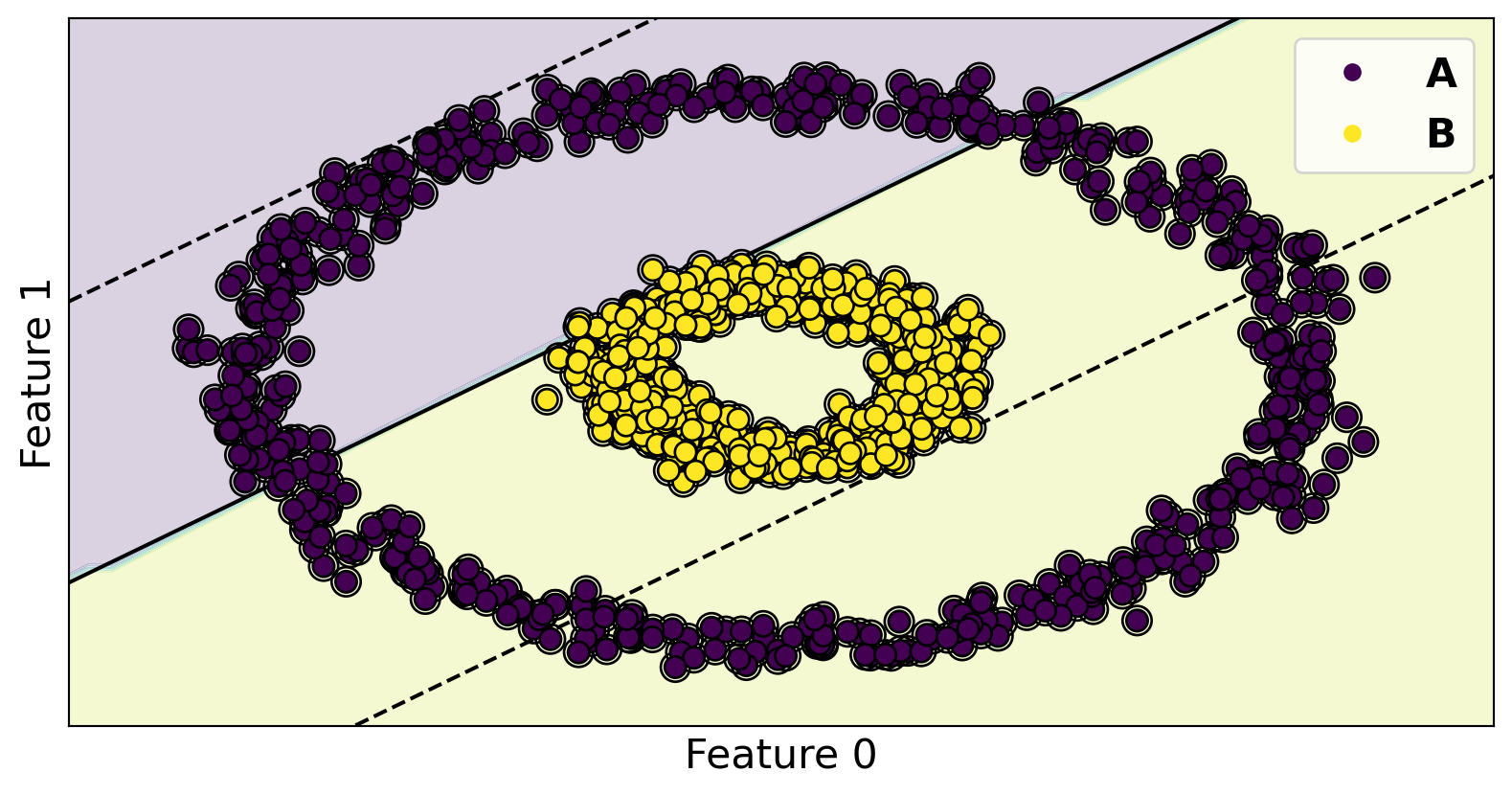
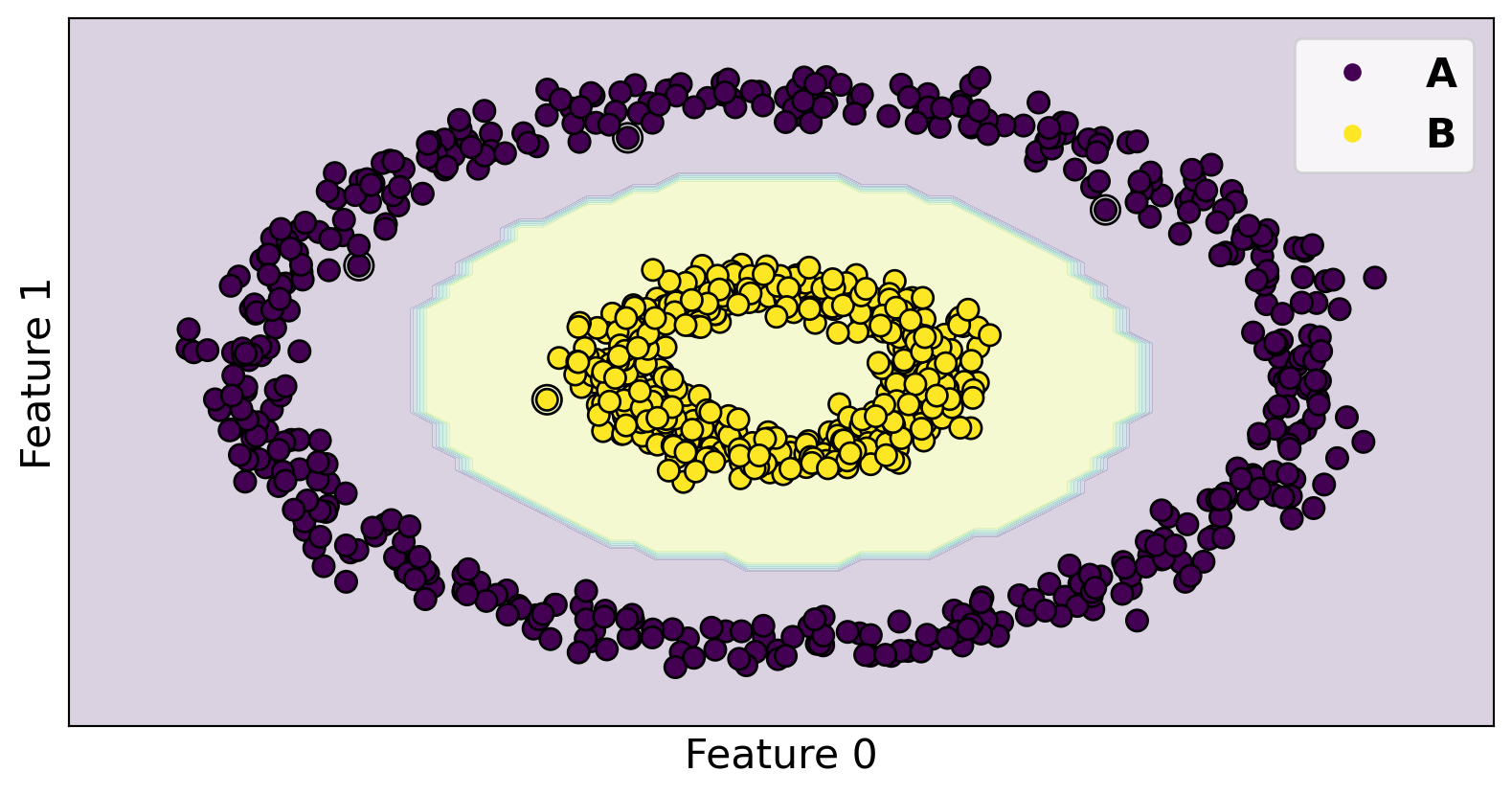
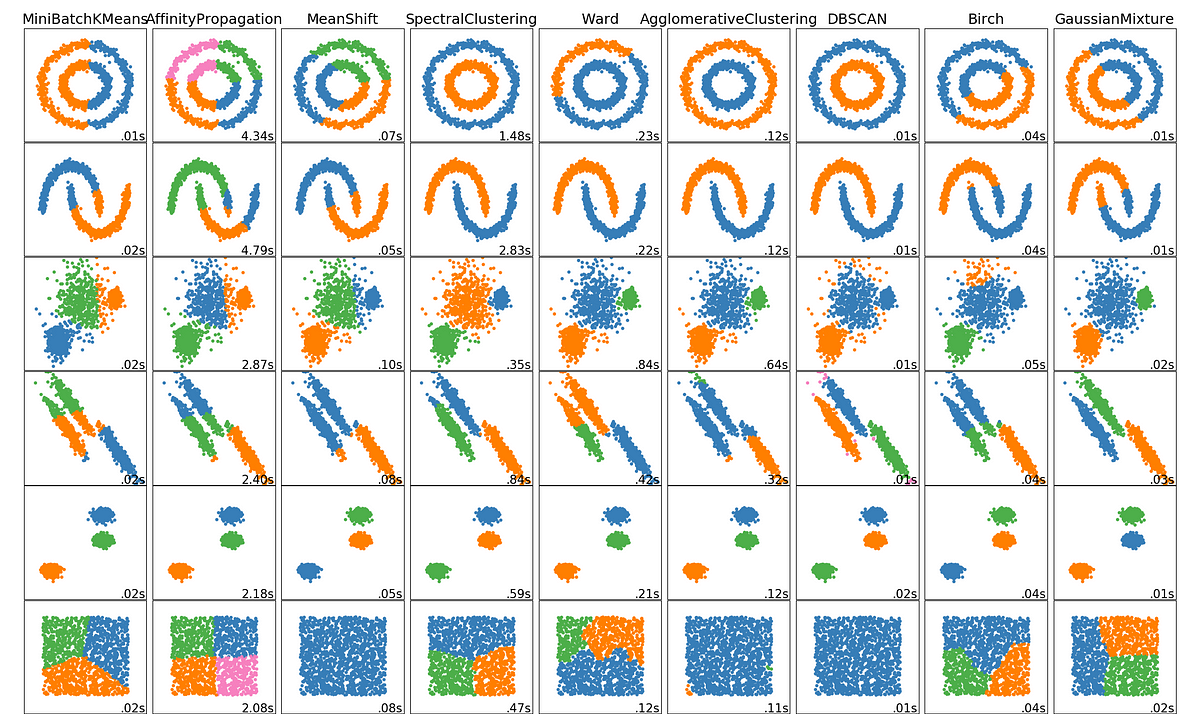
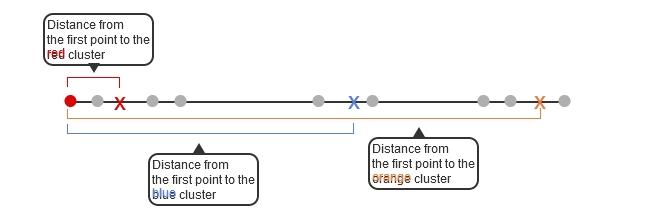
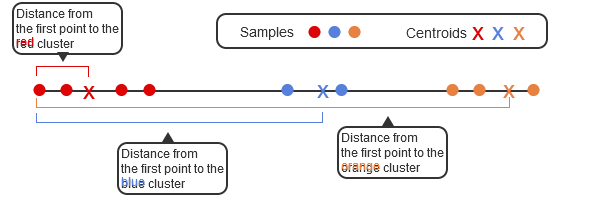
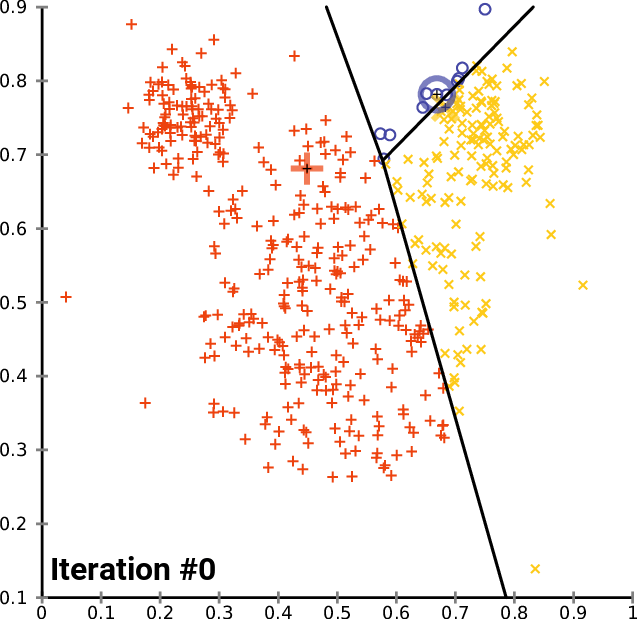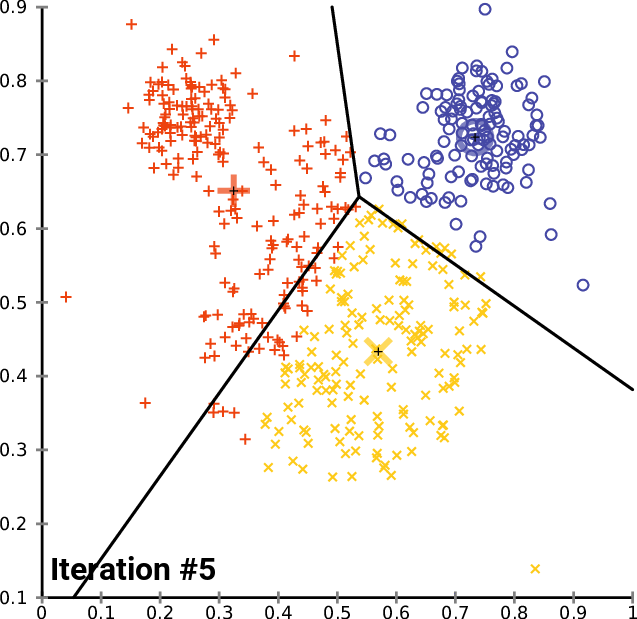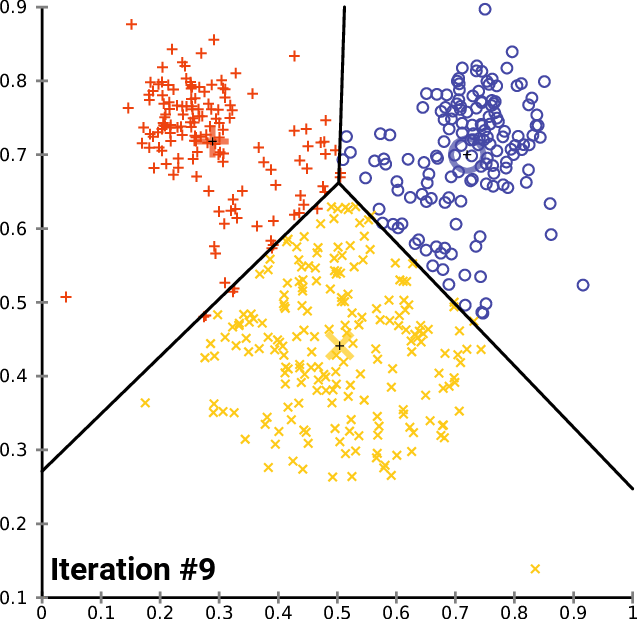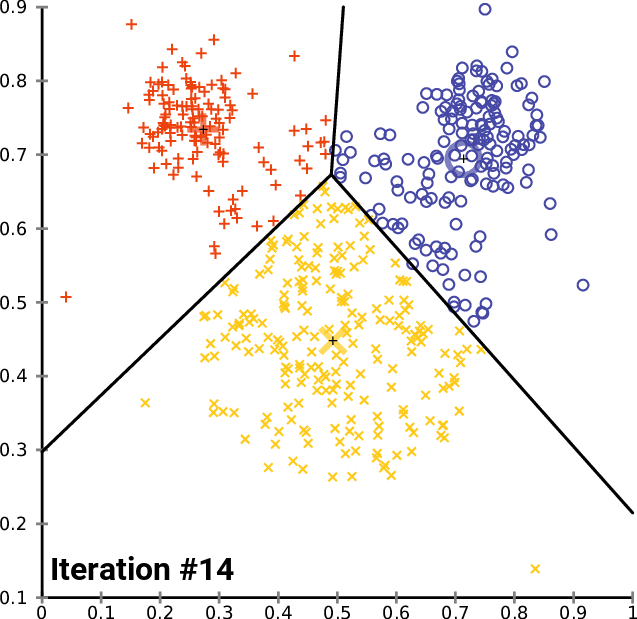
Code
from sklearn import svm
X, Y = make_blobs(random_state=42, n_samples=100, n_features=2, centers=[[-2, 5], [0, 0]], cluster_std=1)
fig, ax = plt.subplots(nrows=1, ncols=1)
model = svm.SVC(kernel="linear", C=10.)
model.fit(X, Y)
plot_svm(X, Y, model, ax=ax, plot_df=False);
# ax.legend(["Class 0", "Class 1"])