CISC482 - Lecture17

Supervised Learning - KNN

Dr. Jeremy Castagno

Class Business

Schedule

  • Reading 7-1: Mar 29 @ 12PM, Wednesday
  • HW5 - Mar 29 @ Midnight, Wednesday
  • Reading 7-2: Mar 31 @ 12PM, Friday
  • HW6 - Working on it… April 12 @ Midnight, Wednesday

Today

  • Review Exam Results
  • Introduction to Supervised Learning
  • KNN

Exam Review

Exam Results

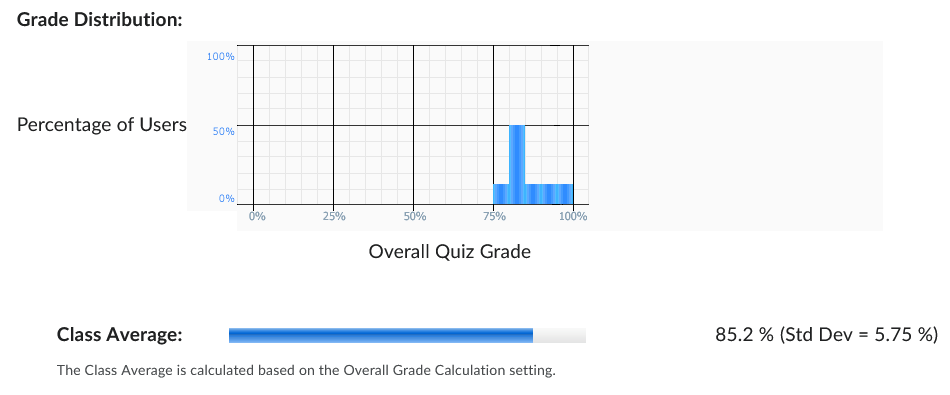
  • Curve: +3 Bonus Points (3 questions, 6% bump)
  • Average: 85%

Top Difficult Questions - #1

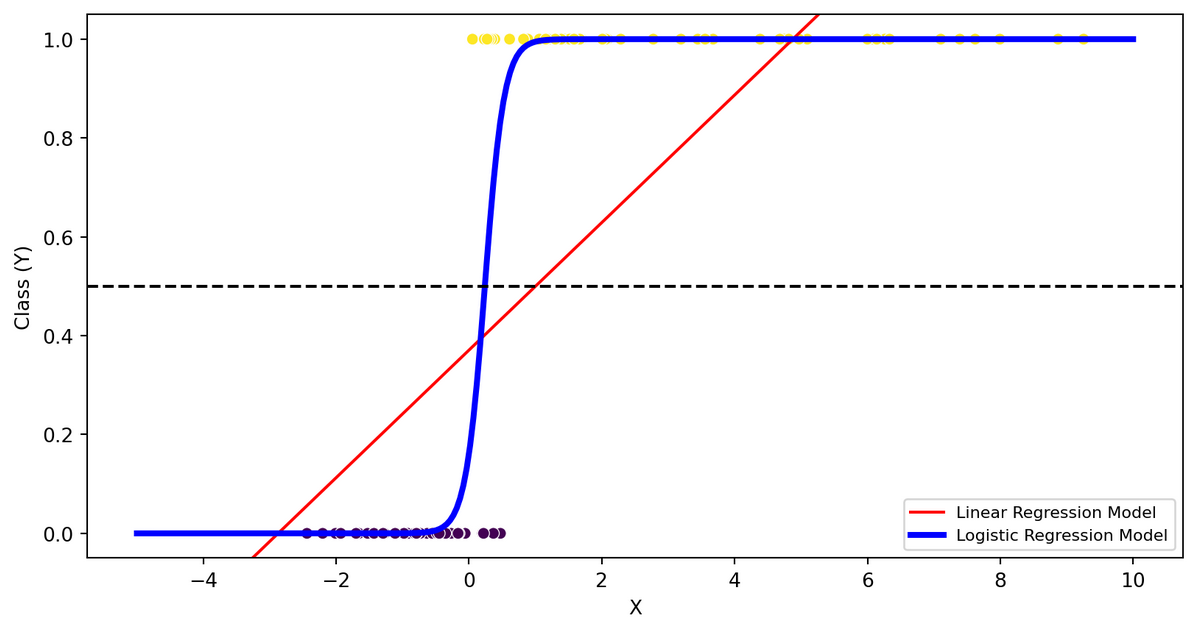
  • Linear model has higher precision
  • Linear model has worse recall
  • Linear model has more FP
  • Linear model has more FN

FN, TP, TN, FP

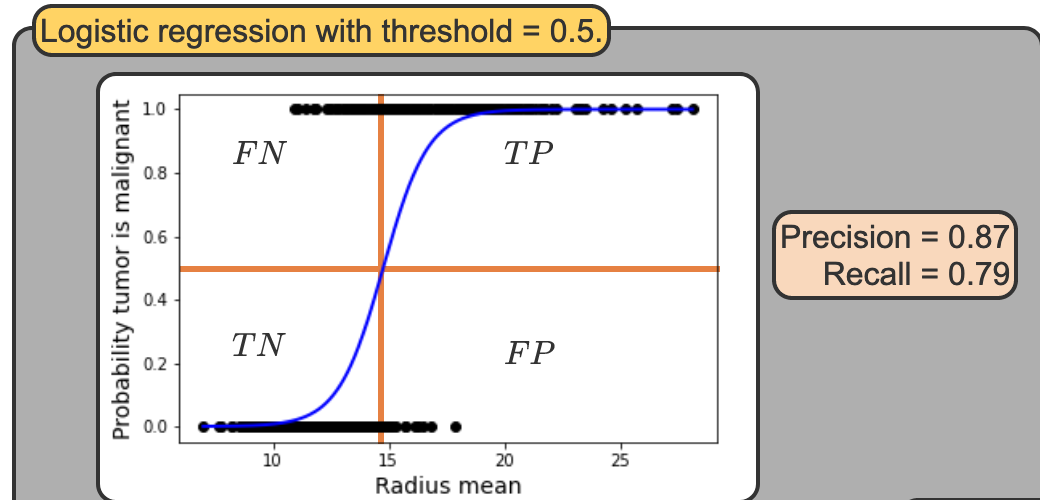
Top Difficult Questions - #2

Select all non-linear functions with respect to model parameters \(\mathbf{\beta}\)

  • \(\beta_0 sin(x)\)
  • \(\beta_0 x^2\)
  • \(\frac{e^{\beta_0 + \beta_1 x}}{1 + e^{\beta_0 + \beta_1 x}}\)
  • \(e^{\beta_0 + \beta_1 x}\)
  • \(sin(\beta_0 x)\)

Top Difficult Questions - #3

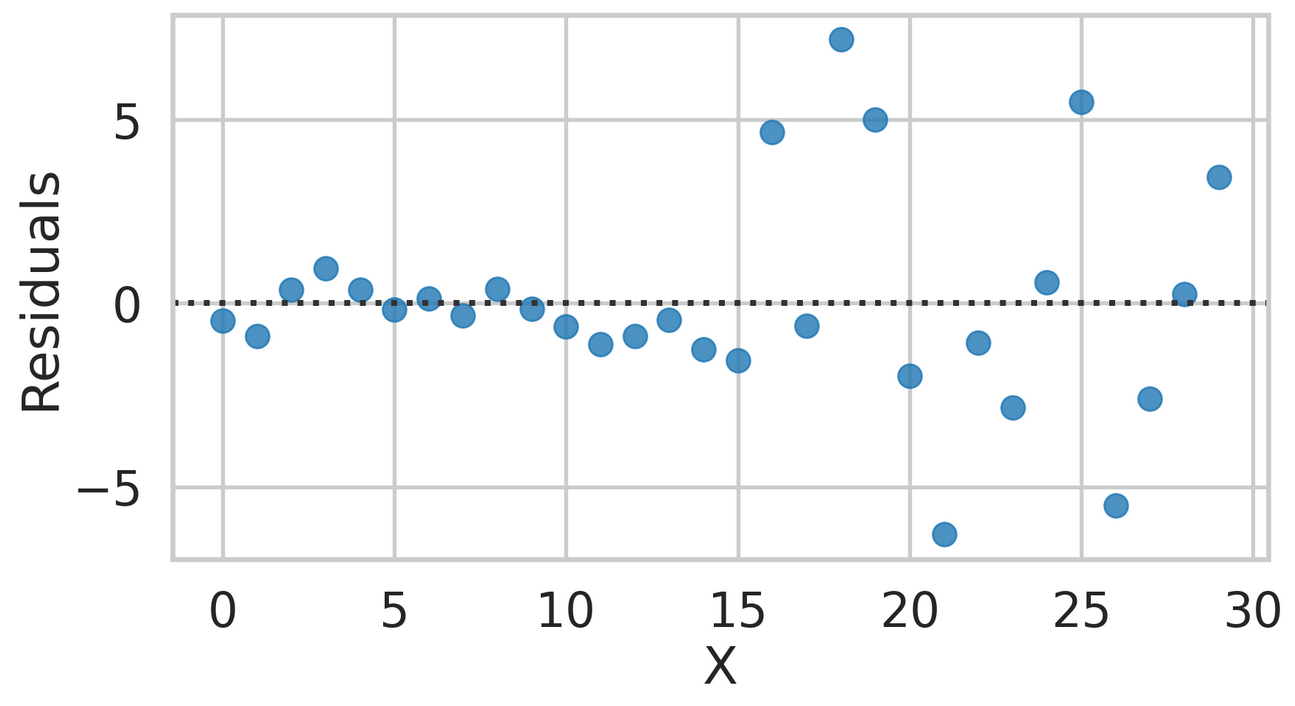
  • Please explain if the assumptions of Linear Regression are met or not.
  • You must discuss at least 3 of the assumptions and clearly explain if each assumption is met from looking at the graph.

Top Difficult Questions - #4

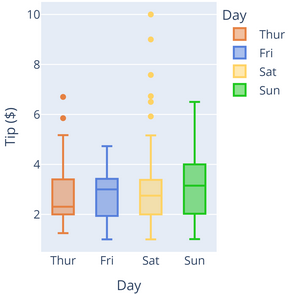
  • Which day had the largest tip?

Big Picture

First 1/4

flowchart LR
    A[Stats and Prob] --> B[Descriptive Statistics]
    A --> C[Distribtuions]
    A --> D[Population Inference]

    E[Data Exploration] --> F[Plotting]
    E --> G[Dataframes]
    E --> H[Exploratory Data Analysis]

First 1/2

flowchart LR
    A[Regression] --> B[Linear Regression]
    A --> C[Mutliple Linear Regression]
    A --> D[Polynomial Regression]
    A --> Z[Logistic Regression]

    E[Model Evaluation] --> F[RMSE, R^2]
    E --> G[Precision, Recall]
    E --> H[Train,Valid,Test ]

Whats next

  • More advanced models!
  • We will still be using what we learned! Especially model evaluation!
  • Fully define concept of supervised learning

Supervised Learning

Terms

  • An instance is labeled if the outcome feature’s value is known for that instance.
  • Supervised learning is training a model to predict a labeled outcome feature based on input features.
  • The outcome feature is also known as the target or dependent variable.
  • The input features are also known as features or independent variables

Example Regression Problem

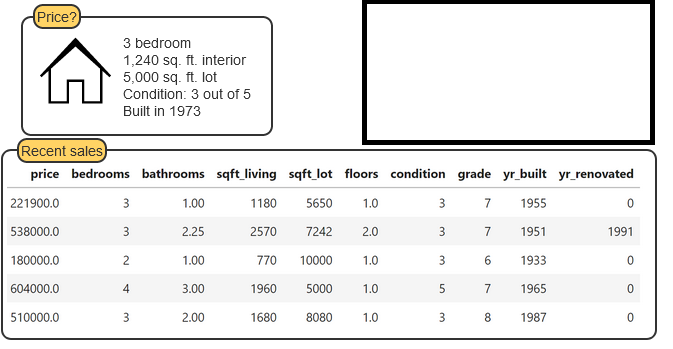
Example Classification Problem

Regression vs Classification

  • Regression - Predicting a continuous numeric outcome
  • Classification - Predicting the class (group) of an instance

Goals of Supervised Learning

  • Predict the values that unlabeled data will have and to explain how the inputs lead to the predicted outputs.

  • A model is interpretable if the relationship between input and output features in the model are easy to explain.

  • A model is predictive if the outcomes produced by the model match the actual outcomes with new data.

What is more important

  • A model can be both predictive and interpretable, but different clients and disciplines value one more than the other.
  • Ex: Scientists value interpretability more to explain the effect of experiments; image recognition models value predictiveness more.
  • A large business may really only care about results. Being predictive may be the only thing that matters

K-nearest Neighbors (KNN)

Introduction

  • k-nearest neighbors (kNN) is a supervised learning algorithm that predicts the output feature of a new instance using other instances that are close for certain input features.
  • A value of k is selected and the k instances with the closest input features are found. The output features of those k instances are used to make the prediction.

Tip

Sometimes, the phrase “birds of a feather flock together” is used to describe the k-nearest algorithm, meaning the algorithm assumes that instances with similar inputs will have similar outputs.

Motivation

Example

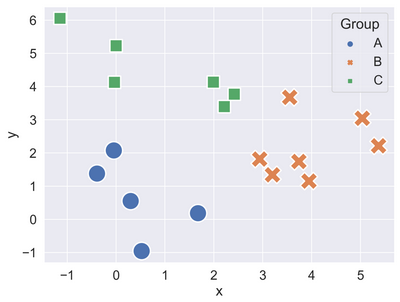
  • (4, 2.5)
  • (0, 4)
  • (2, 1)

Finding your nearest neighbors

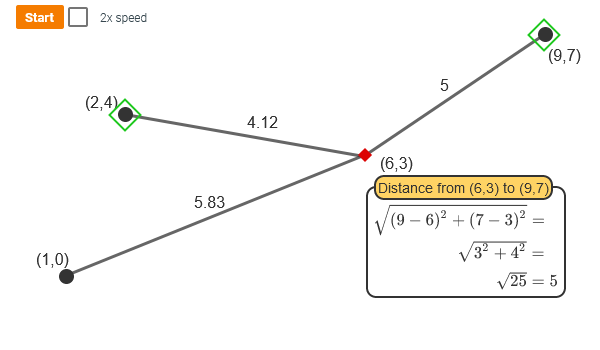
  • How do determine how close a point is form the another (metric)
  • distance(x,y) = \(\sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + ... + (x_p - y_p)^2 }\)
  • Distance Calculation

Using KNN for Classification

Regression with KNN

  1. Select k, the number of neighbors to consider.
  2. Calculate the distance between all labeled instances and the instance to predict.
  3. The k instances with the shortest distances are the nearest neighbors.
  4. Predict by averaging the k nearest neighbors’ output values.

Software

scikit-learn

Example - Data

Code 
X, y = make_blobs(n_samples=100, centers=2, cluster_std=1.5, n_features=2,
                  random_state=0)
c_names = ["Class 0", "Class 1"]
fig, ax = plt.subplots(nrows=1, ncols=1)
scatter = ax.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis');
ax.legend(handles=scatter.legend_elements()[0], 
           labels=c_names,
           title="Class")
<matplotlib.legend.Legend at 0x7f12d8dd24d0>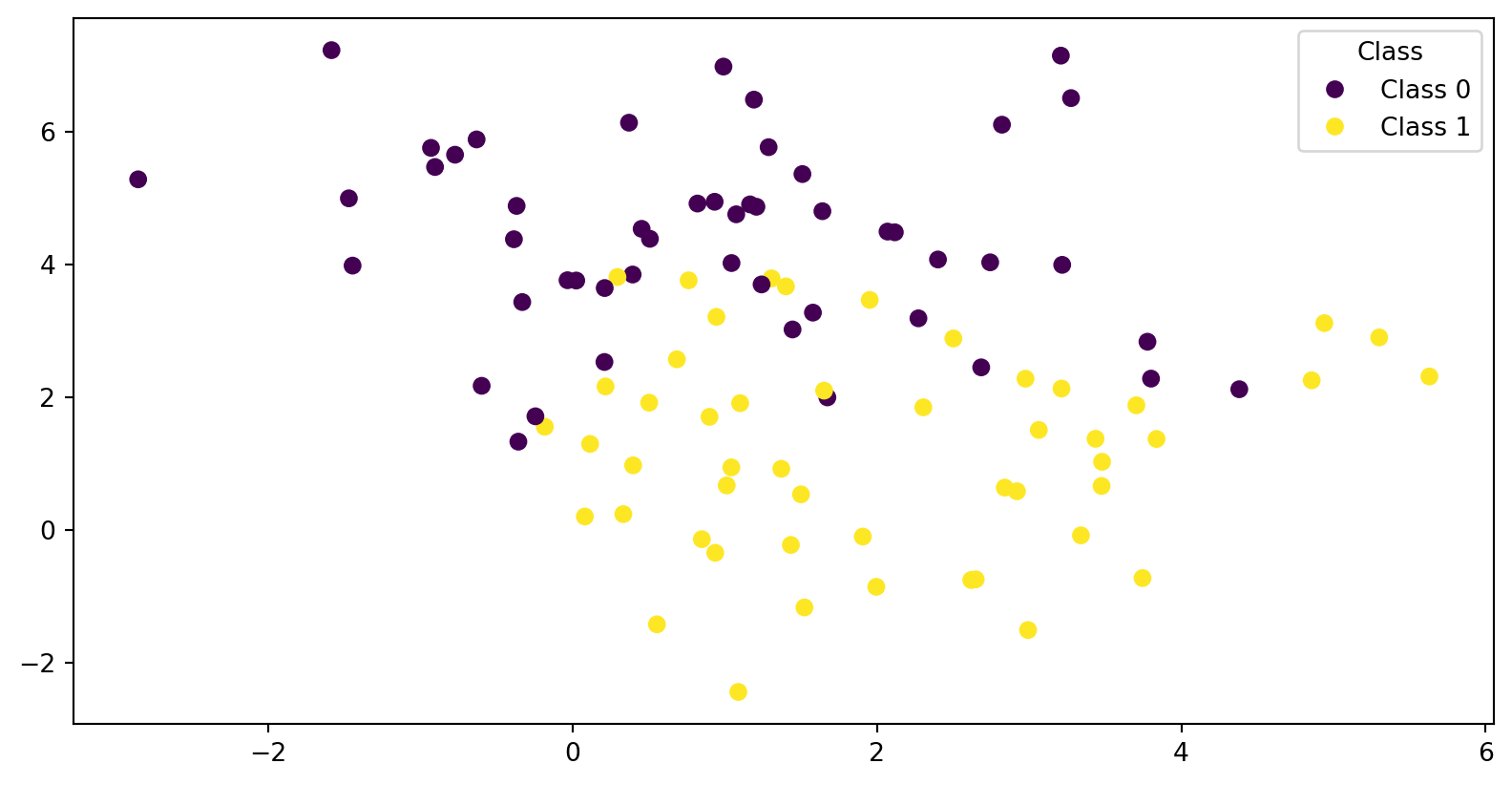

Split into Train and Test

Code 
from sklearn.model_selection import train_test_split
# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=0)

# Plot data
fig, ax = plt.subplots(nrows=1, ncols=2)

data = [(X_train, y_train, 'Train Set'), (X_test, y_test, 'Test Set')]
for (X, y, title), ax_ in zip(data, ax):
  scatter = ax_.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis')
  ax_.set_title(title)
  ax_.set_xlabel("X0")
  ax_.set_ylabel("X1")
  ax_.legend(handles=scatter.legend_elements()[0], 
           labels=c_names,
           title="Class")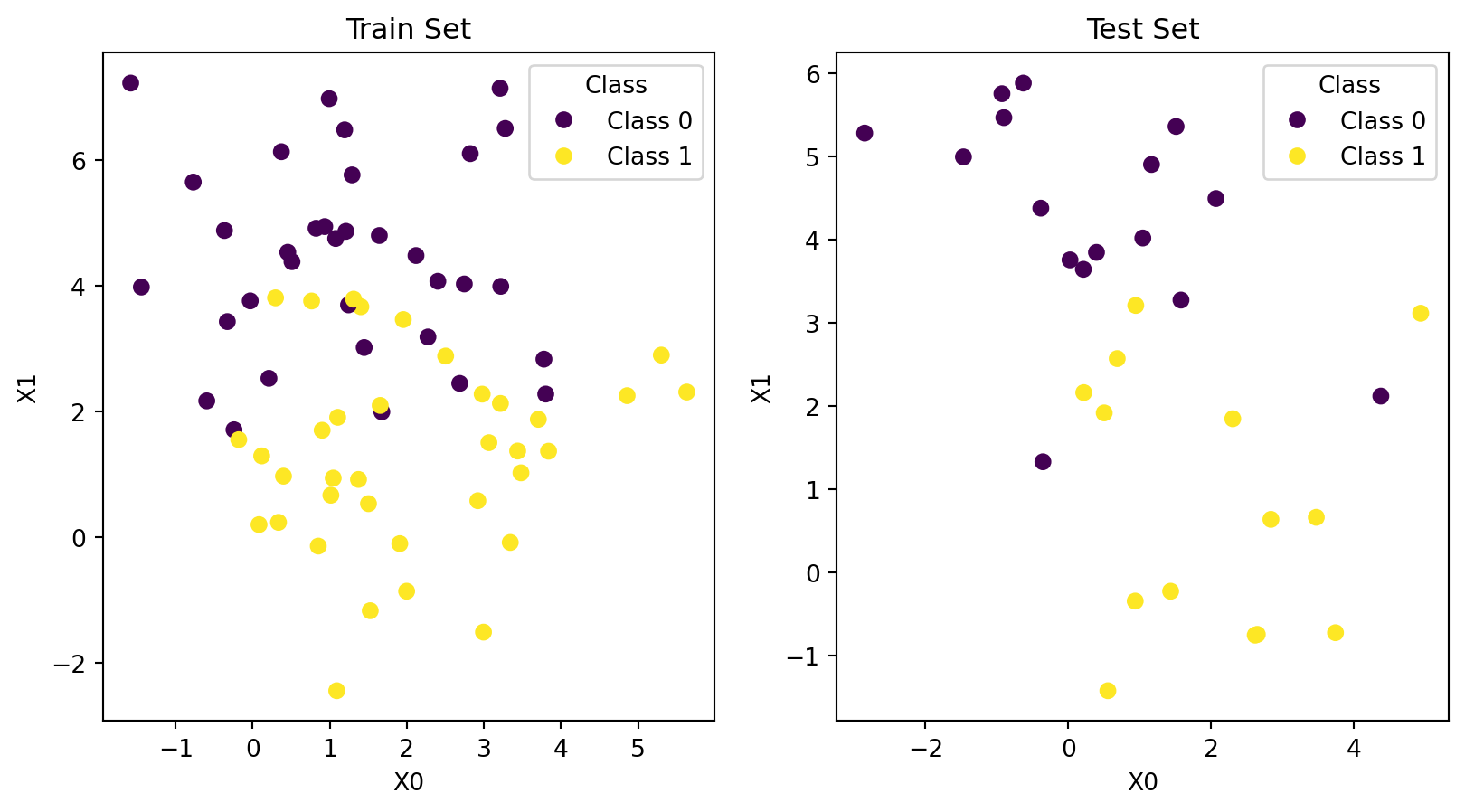

Train Model, Sanity Check

Code 
from sklearn.neighbors import KNeighborsClassifier
# Create and train model
model = KNeighborsClassifier(n_neighbors=5)
model.fit(X_train, y_train)

# Single point sanity check
test_point = [2, 1]
predicted_group = model.predict([test_point])
print(f"We predict that {test_point} will belong to class: {predicted_group}")
We predict that [2, 1] will belong to class: [1]

Test Model

Code 
# Make predictions
predictions = model.predict(X_test)

# Plot data
fig, ax = plt.subplots(nrows=1, ncols=2)
data = [(X_test, y_test, 'Test Set (Ground Truth)'), (X_test, predictions, 'Test Set Predicted')]
for (X, y, title), ax_ in zip(data, ax):
  scatter = ax_.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis')
  ax_.set_title(title)
  ax_.set_xlabel("X0")
  ax_.set_ylabel("X1")
  ax_.legend(handles=scatter.legend_elements()[0], 
           labels=c_names,
           title="Class")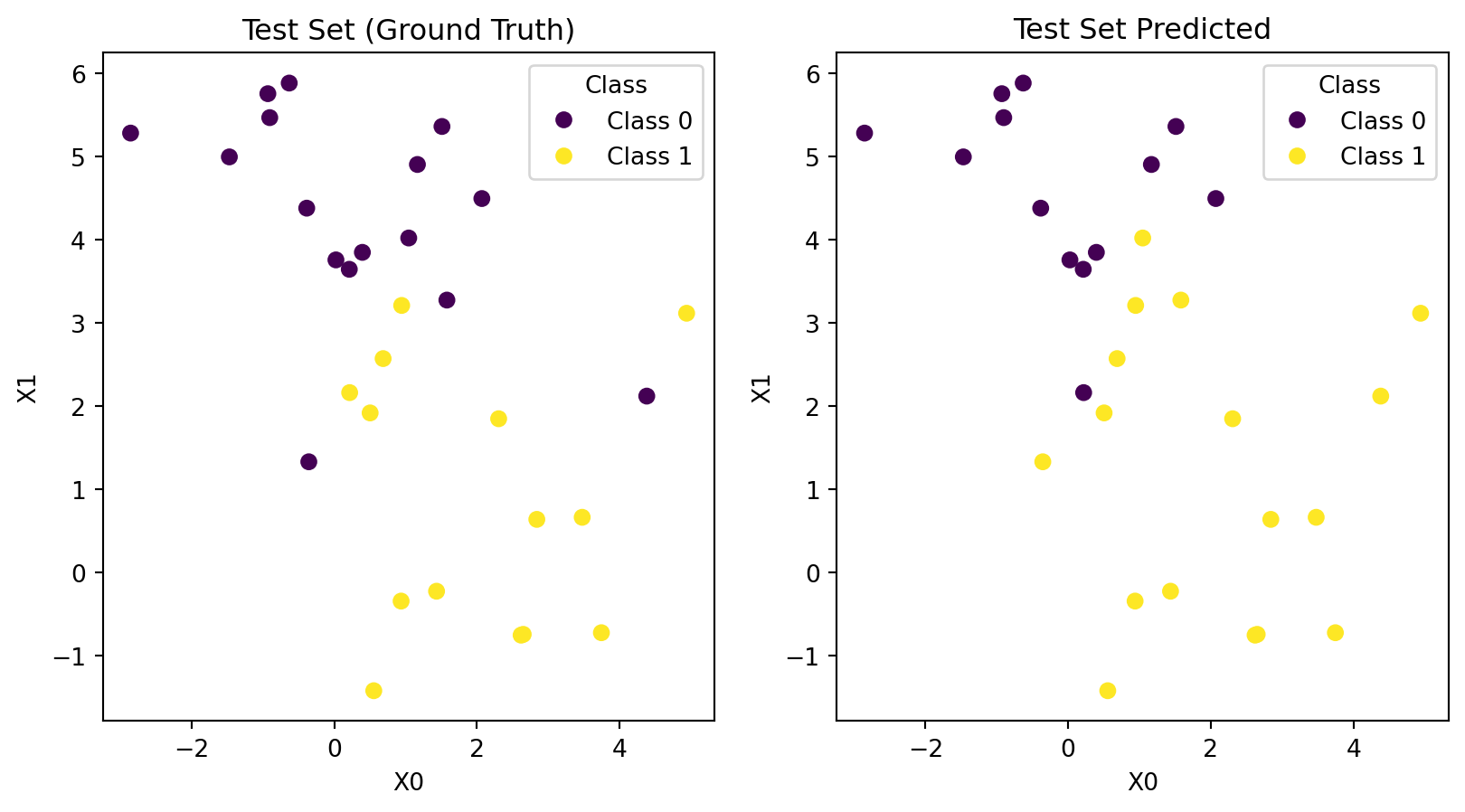

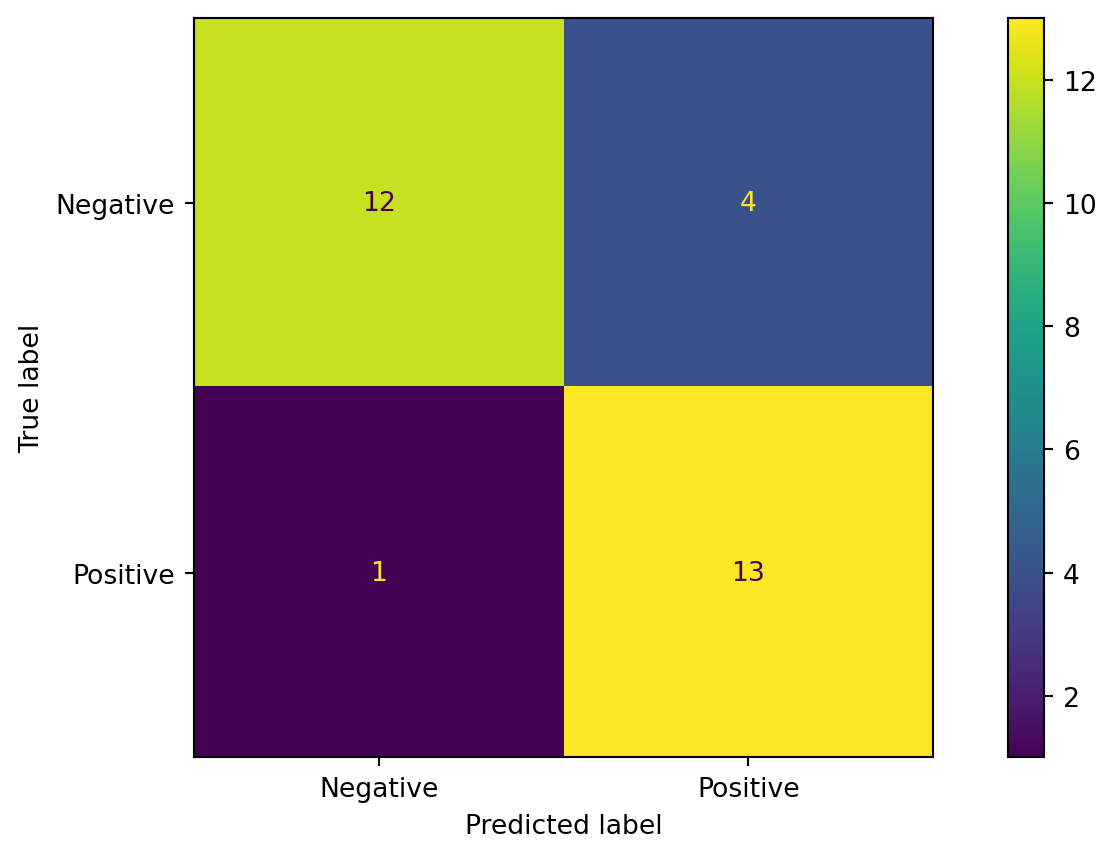
Confusion Matrix, Plot

Code 
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay

cm = confusion_matrix(y_test, predictions)
disp = ConfusionMatrixDisplay(confusion_matrix=cm,
                              display_labels=['Negative', 'Positive'])
disp.plot()

plt.show()

Confusion Matrix
[[12  4]
 [ 1 13]]

Classication Metrics

  • Accuracy = \(\frac{TP+TN}{TP+TN+FP+FN}\)
  • Precision = \(\frac{TP}{TP+FP}\)
  • Recall = \(\frac{TP}{TP+FN}\)
  • F1 = \(\frac{2*Precision*Recall}{Precision+Recall} = \frac{2*TP}{2*TP+FP+FN}\)

Classification Report

Code 
from sklearn.metrics import classification_report
report = classification_report(y_test, predictions, target_names=["Negative", "Postive"])
print(report)
              precision    recall  f1-score   support

    Negative       0.92      0.75      0.83        16
     Postive       0.76      0.93      0.84        14

    accuracy                           0.83        30
   macro avg       0.84      0.84      0.83        30
weighted avg       0.85      0.83      0.83        30

https://jeremybyu.github.io/intro-ds-website