CISC482 - Lecture16

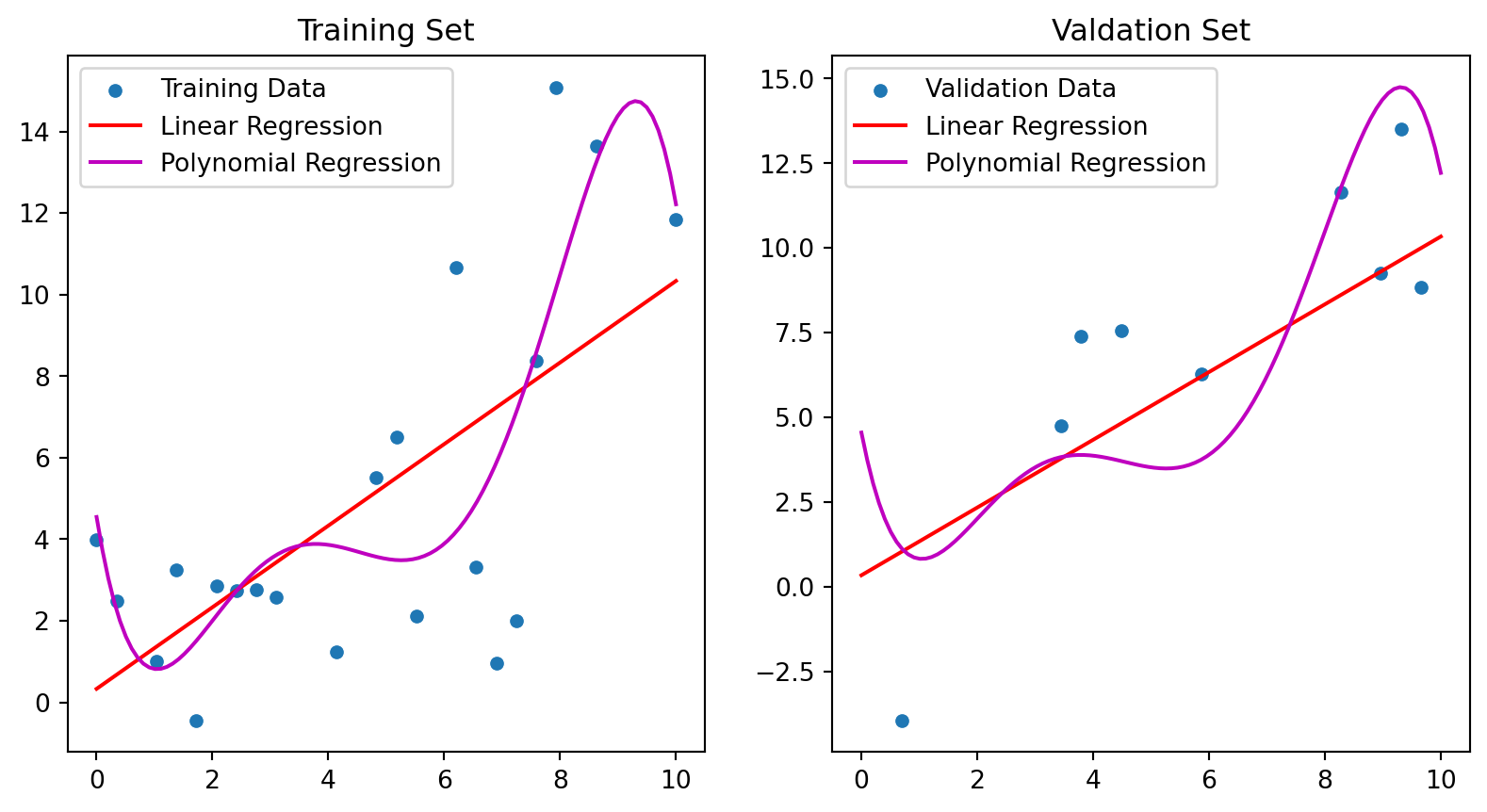
Evaluating Model Performance - Bootsrapping

Dr. Jeremy Castagno

Class Business

Schedule

• Reading 6-3: Mar 22 @ 12PM, Wednesday
• Proposal: Mar 22, Wednesday
• Propsal Template!
• HW5 - Mar 29 @ Midnight, Wednesday

Today

• Review Train/Valid/Test
• Review K-Folds

Review

Purpose of model evaluation

• \(R^2\), \(recall\), etc. tells us how our model is doing to predict the data we already have
• But generally we are interested in prediction for a new observation,
• We have a couple ways of simulating out-of-sample prediction before actually getting new data to evaluate the performance of our models

Splitting Data

• Train/Test/Valid
  • Train (70% of data) - Used to fit a model or multiple models
  • Validation (15% of data) - Used to compare different models
  • Test (15% of data) - Final model evaluation

Train/Valid Split

TRAIN SET - Linear Model R^2 = 0.44; Polynomial Model R^2 = 0.62
VALID SET - Linear Model R^2 = 0.65; Polynomial Model R^2 = 0.41

K-folds Cross Validation

• Split data into Train(80%)/Test(20%)
• Break the Train data into k groups.
• Train/Validate across the goups

K-Folds Split (k=10)

K-Folds Train and Validate

Bootrapping

What is it?

• Bootstrapping is the process of generating simulated samples by repeatedly drawing with replacement from an existing sample.
• Bootstrap samples are often used to evaluate a statistic’s ability to estimate a parameter.
• This process can give you a distribution of estimates!

Bootstrapping starts with a single sample

• Population may have an unknown n
• We have one sample from the population. How many observations do we have in this sample?

Repeated sampling with replacement

Example - Flipper Length vs Body Mass

Code

df = df[['flipper_length_mm', 'body_mass_g']]
df.head()

	flipper_length_mm	body_mass_g
0	181.00	3,750.00
1	186.00	3,800.00
2	195.00	3,250.00
4	193.00	3,450.00
5	190.00	3,650.00

Code

sns.regplot(data=df, x='flipper_length_mm', y='body_mass_g', ci=None);

Bootrapping

Code

n_boots = 100 # number of bootrap iterations
n_points = int(len(df) * 0.50) # sample size with replacement
boot_slopes = [] # store regressed line slopes
boot_intercepts = [] # store regressed line intercepts
plt.figure() # creates a figure that we can plot *multiple* times
linear_model = LinearRegression()
for _ in range(n_boots):
 # sample the rows, same size, with replacement
 sample_df = df.sample(n=n_points, replace=True)
 # fit a linear regression
 linear_model.fit(sample_df[['flipper_length_mm']], sample_df['body_mass_g'])
 # append regressed coefficients
 boot_intercepts.append(linear_model.intercept_)
 boot_slopes.append(linear_model.coef_[0])
 # plot a greyed out line of the prediction
 y_pred_temp = linear_model.predict(sample_df[['flipper_length_mm']])
 plt.plot(sample_df['flipper_length_mm'], y_pred_temp, color='grey', alpha=0.2)# add data points

plt.scatter(sample_df['flipper_length_mm'], sample_df['body_mass_g'])
plt.grid(True)
plt.xlabel('Flipper Length')
plt.ylabel('Body Mass')
plt.title(f'Bootrapping; Bootstrap interations={n_boots}; Sample Size:{n_points}')
plt.show();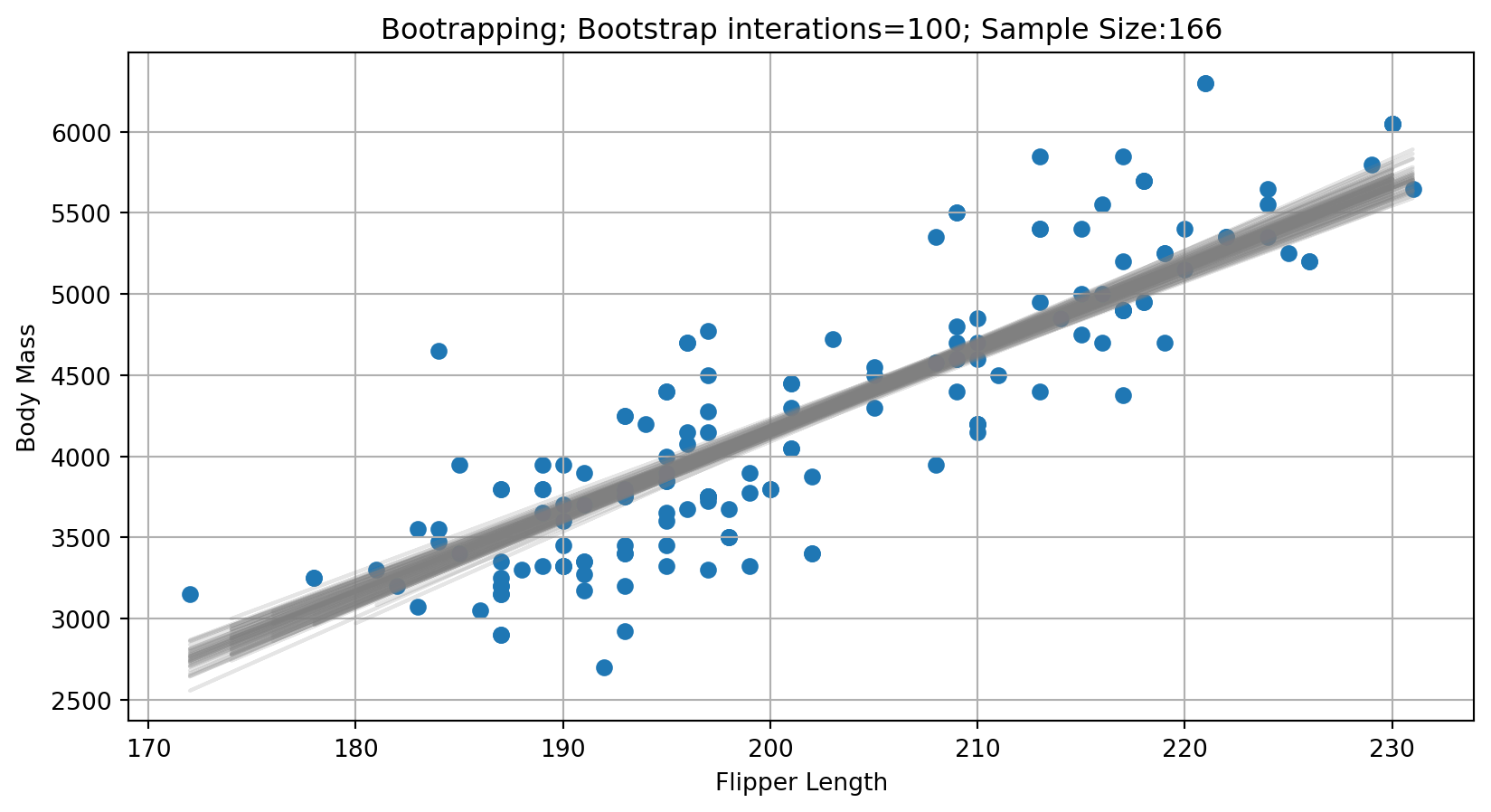

How consistent are the predictions for different samples?

Historgram of Model Parameters!

Code

df_p = pd.DataFrame(dict(slope=boot_slopes, intercept=boot_intercepts))
sns.displot(data=df_p, x='slope');

Code

sns.displot(data=df_p, x='intercept');

Inferential Statisitcs

• Since we have a distribution of these popluation parameters we can calculate their mean and variance
  • The mean will be the best estimator
  • The variance can be used to calcluate our confidence in the result
• How do we calculate confidence interval?
  • \(\bar{x} \pm 1.96 \frac{\sigma}{\sqrt{n}}\)

Model Selection

One Standard Error Method

• Select a few different models you want to try out (linear regression, polynomial regressions, multivariable regression, etc.)
• Perform K-folds cross validation on each of these models.
• Each model will have a distribution for error, mean and variance.
• Find the model with the minimum mean score
• Then select the simplest model whose mean score falls within one standard deviation.

Example One

Example Two

Exam Review

Ask your Questions!