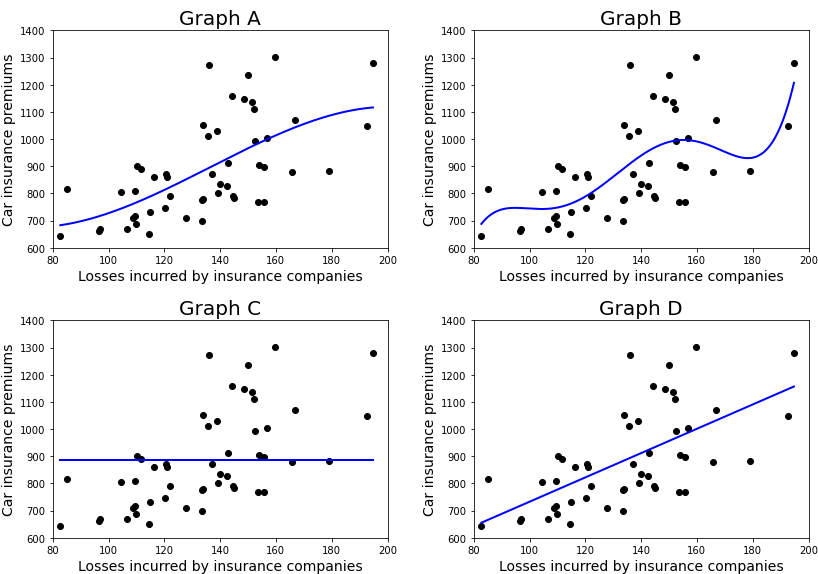
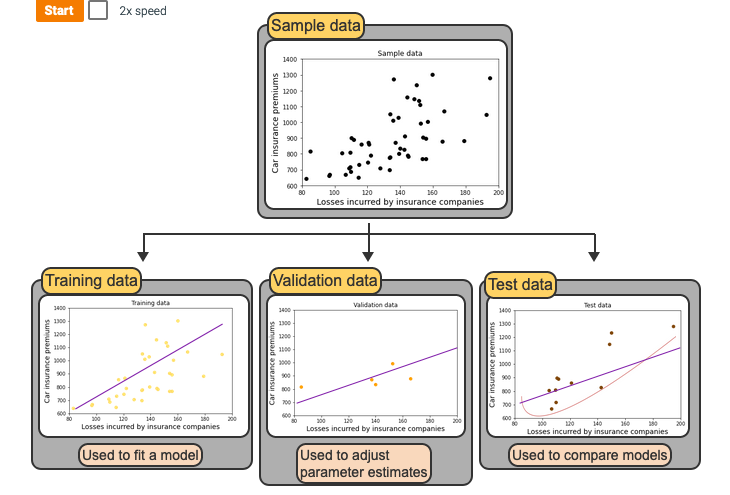
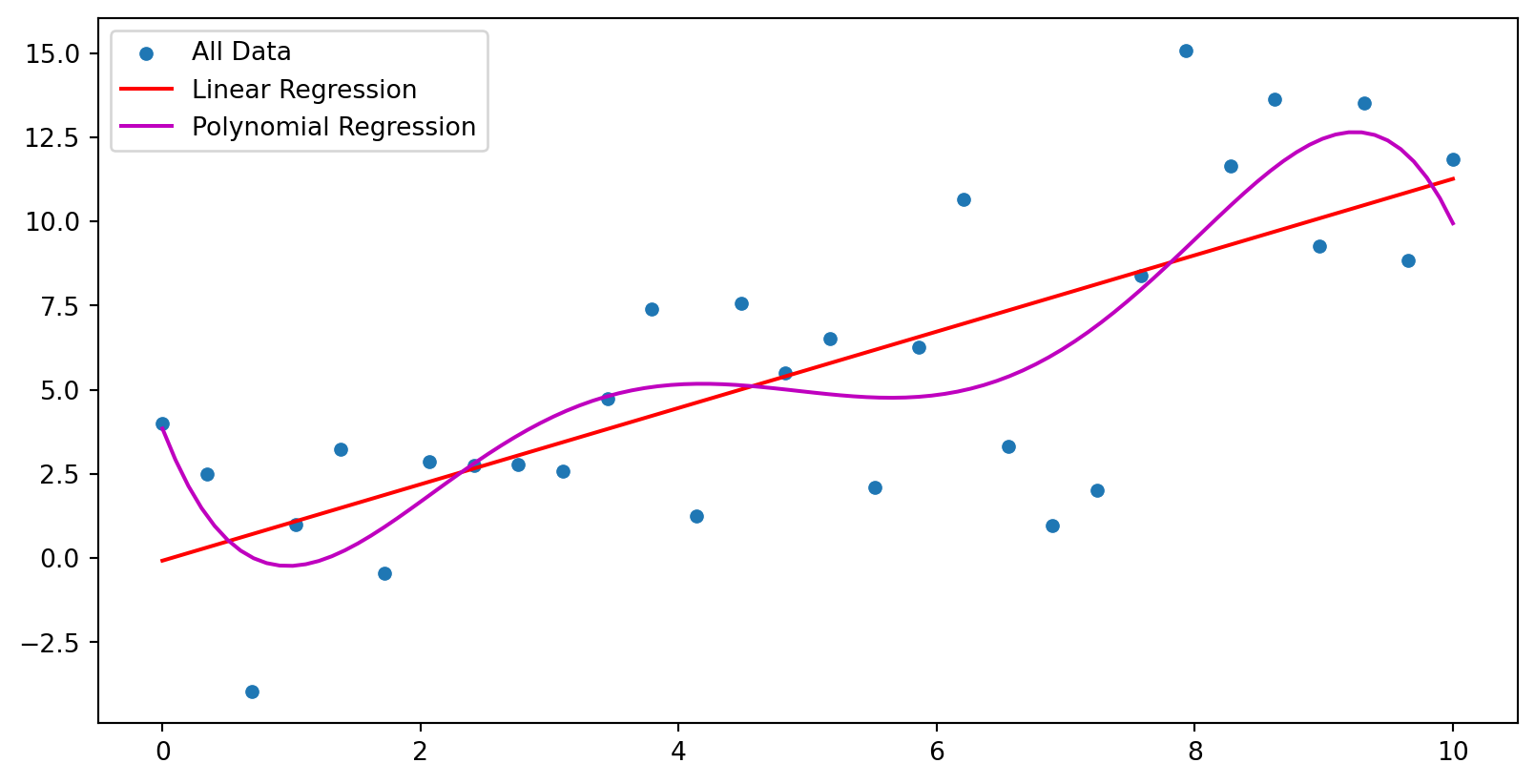
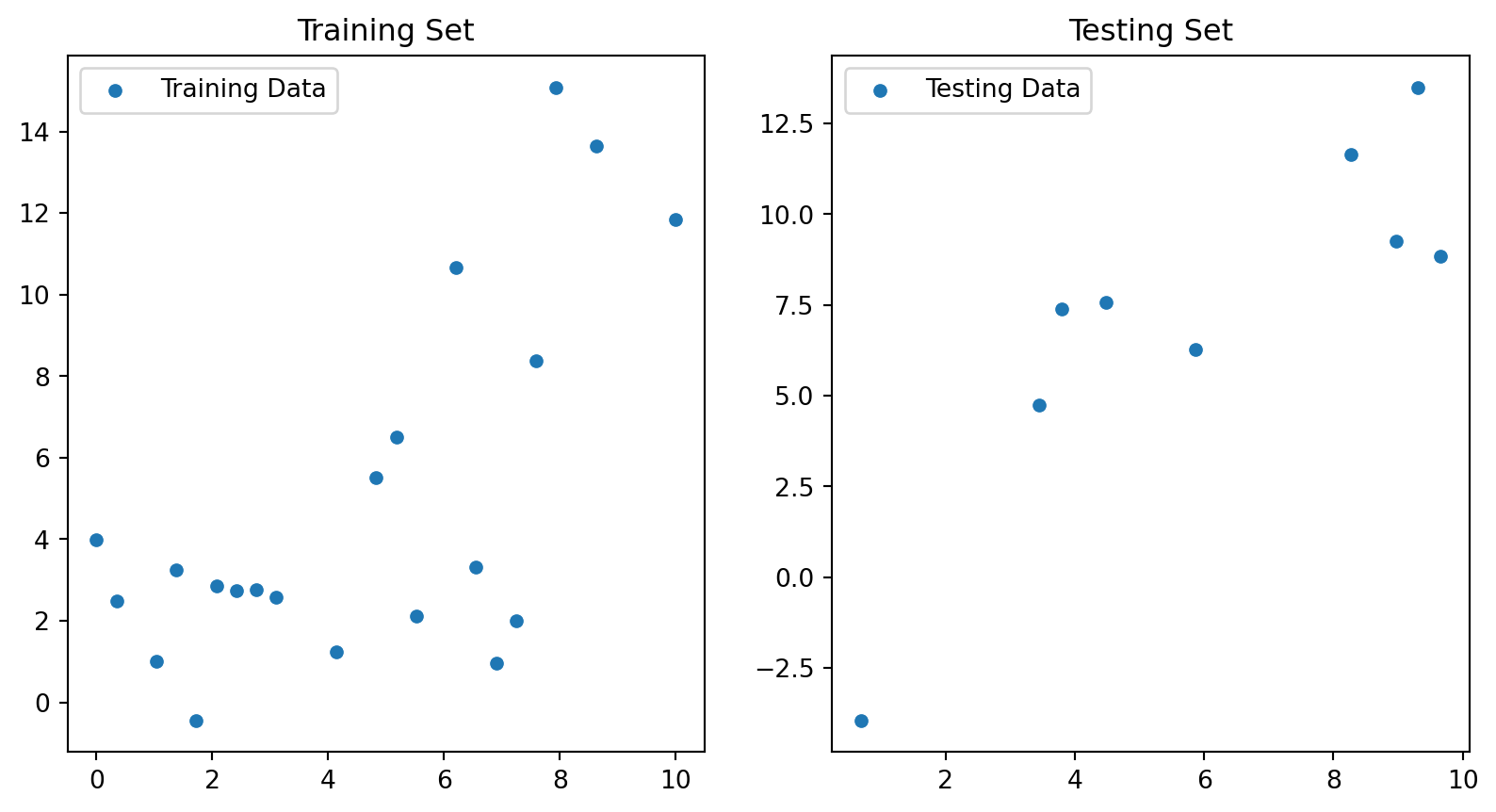
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.30, random_state=0)
linear_model.fit(X_train, y_train)
quadratic_model = np.poly1d(np.polyfit(X_train[:,0], y_train, degree)) # quadratic
print(f"TRAIN SET - Linear Model R^2 = {r2_score(y_train, linear_model.predict(X_train)):.2f}; Polynomial Model R^2 = {r2_score(y_train, quadratic_model(X_train[:,0])):.2f}")
print(f"TEST SET - Linear Model R^2 = {r2_score(y_test, linear_model.predict(X_test)):.2f}; Polynomial Model R^2 = {r2_score(y_test, quadratic_model(X_test[:,0])):.2f}")
fig, ax = plt.subplots(nrows=1, ncols=2) # create 2 plots!
# Plot training result
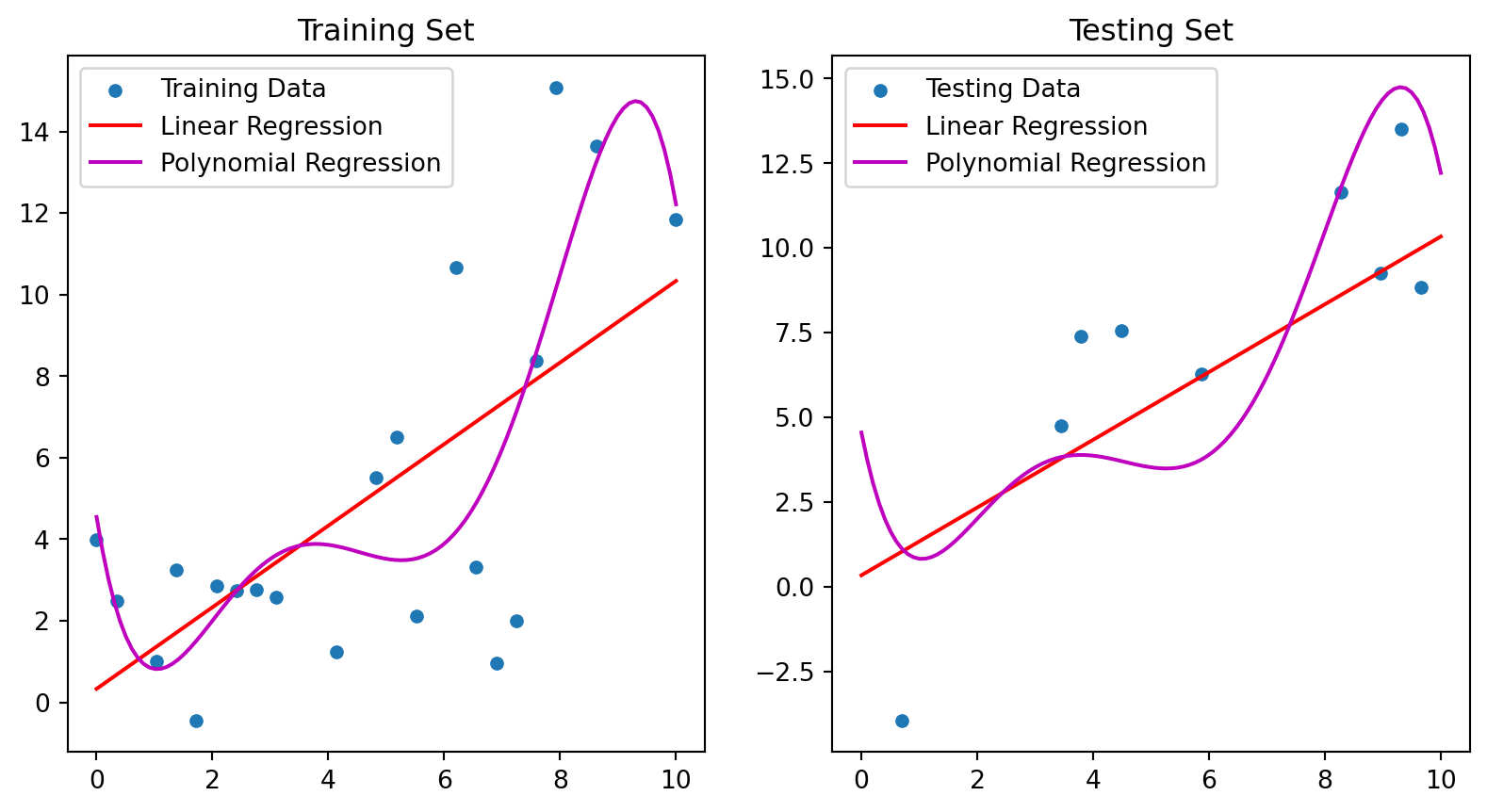
x_graph = np.linspace(0, 10, 100)
sns.scatterplot(x=X_train[:,0], y=y_train, ax=ax[0], label="Training Data")
ax[0].plot(x_graph, linear_model.predict(x_graph[:, np.newaxis]), color='r', label='Linear Regression')
ax[0].plot(x_graph, quadratic_model(x_graph), color='m', label='Polynomial Regression');
# ax[0].scatter(np.sort(X_train[:, 0]), quadratic_model(np.sort(X_train[:, 0])), color='m');
ax[0].set_title("Training Set")
ax[0].legend()
# Plot testing result
sns.scatterplot(x=X_test[:,0], y=y_test, ax=ax[1], label="Testing Data")
ax[1].plot(x_graph, linear_model.predict(x_graph[:, np.newaxis]), color='r', label='Linear Regression')
ax[1].plot(x_graph, quadratic_model(x_graph), color='m', label='Polynomial Regression');
# ax[1].scatter(np.sort(X_test[:, 0]), quadratic_model(np.sort(X_test[:, 0])), color='m');
ax[1].set_title("Testing Set")
ax[1].legend();