CISC482 - Lecture10

Regression

Dr. Jeremy Castagno

Class Business

Schedule

Topic Ideas - Feb 22 @ Midnight
Reading 5-1: Feb 22 @ 12PM, Wednesday
Reading 5-2: Feb 24 @ 12PM, Friday
Reading 5-3: Mar 01 @ 12PM, Wednesday

Today

Introduction to Regression
Review Topic Ideas
More Exploratory Data Analysis

Introduction to Regression

Input and Output

An input feature takes values without being impacted by any other features.
An output feature has values that vary in response to variation in some other feature(s).
- We often called this the response variable
In an experiment, input features are often controlled by researchters, and output features are observed
We often visualize these with scatter plots

Example Data

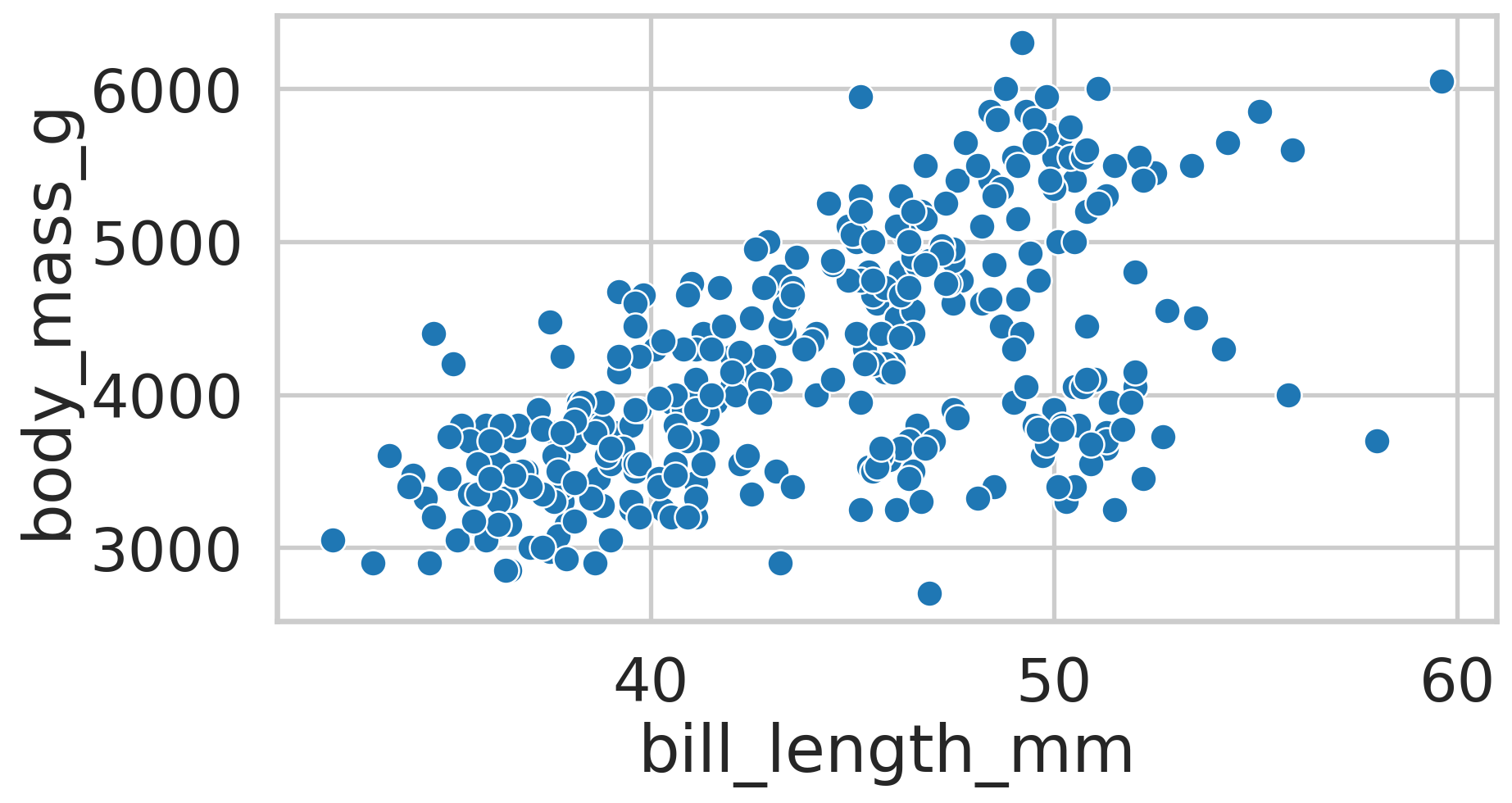
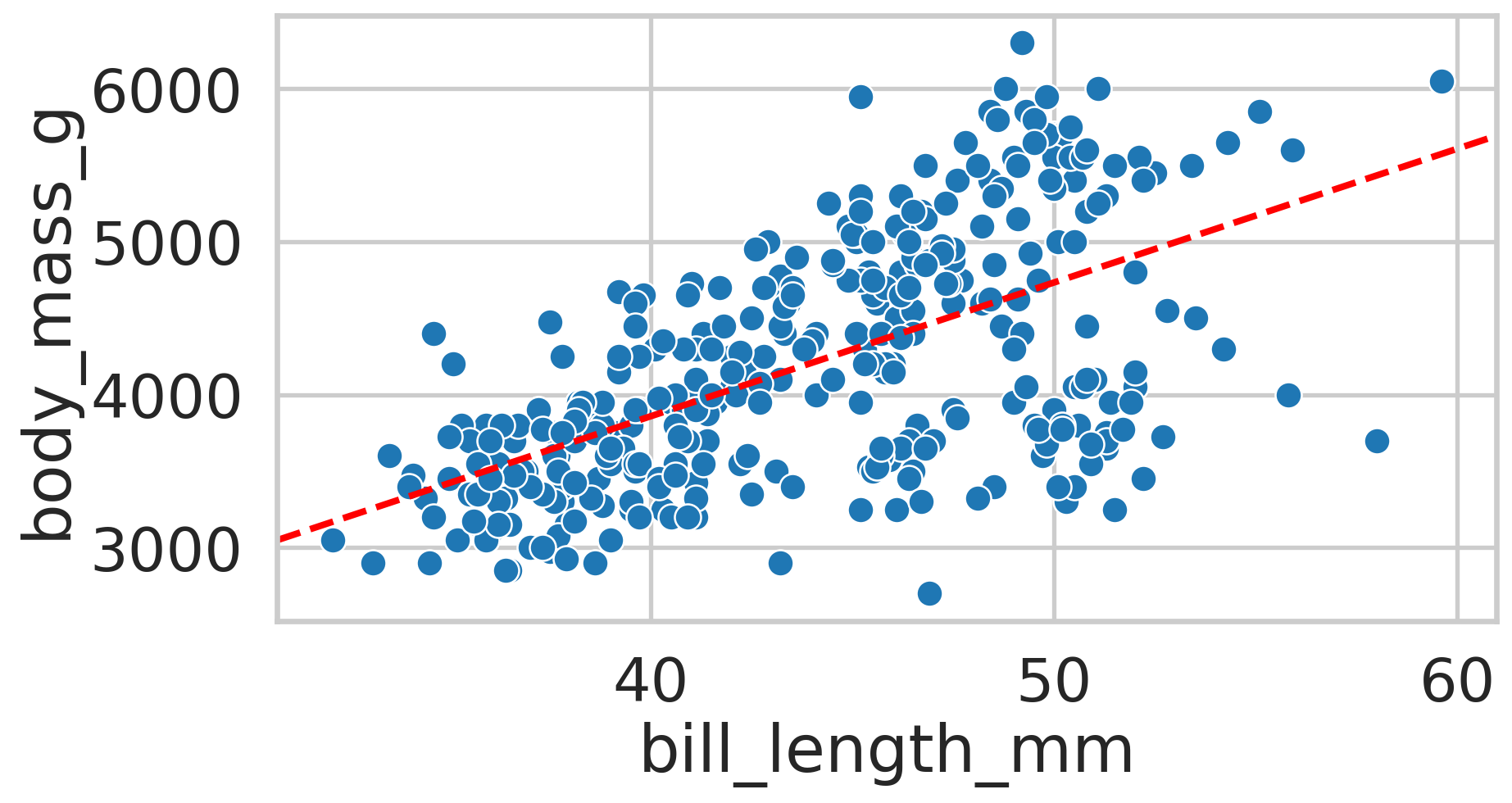
	species	island	bill_length_mm	bill_depth_mm	flipper_length_mm	body_mass_g	sex	year
0	Adelie	Torgersen	39.10	18.70	181.00	3,750.00	male	2007
1	Adelie	Torgersen	39.50	17.40	186.00	3,800.00	female	2007
2	Adelie	Torgersen	40.30	18.00	195.00	3,250.00	female	2007
3	Adelie	Torgersen	NaN	NaN	NaN	NaN	NaN	2007
4	Adelie	Torgersen	36.70	19.30	193.00	3,450.00	female	2007

Scatter Plot

Correlation: 0.60

Describing

The direction: positive if larger values of one feature correspond to larger values of the other feature.
The form: linear pattern or a nonlinear pattern. Sometimes two features may not have an obvious form.
The strength: how closely the observations in a scatter plot follow the form’s pattern.

Questions

Correlation

Correlation is a statistical measure that expresses the extent to which two variables are linearly related
They change together at a constant rate
It’s a common tool for describing simple relationships without making a statement about cause and effect.
Range from -1 to 0 to +1

Regression Model

A model for an output feature \(y\) using input feature(s) \(X\) is a function \(f(X)\) that predicts an expected value \(\hat{y}\) for a given value of \(X\).and
\(\hat{y} = f(X)\)
A regression model is one that has a numerical output feature and input features.

Regression Example

What is the error of our model (Residual)

Simple Linear Regression

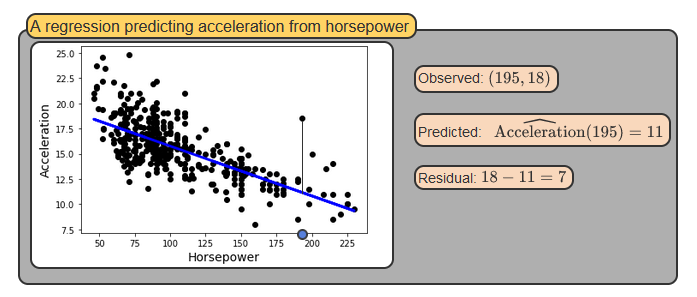
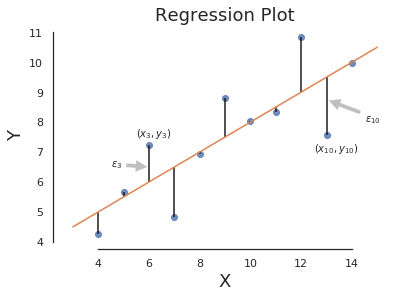
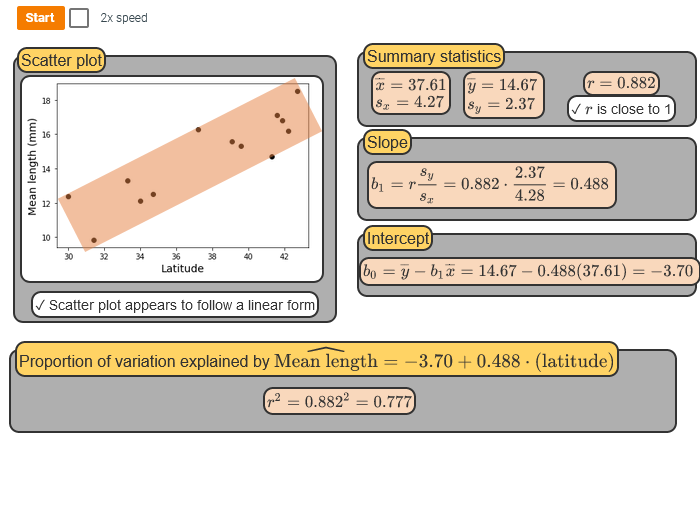
Main Equation

Set of data: \(\{(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\}\)
- x: input, y: output
Model: \(\hat{y} = \beta_0 + \beta_1 x + \epsilon\)
- \(\hat{y}\) = prediction
- \(\beta_0\) = y-intercept
- \(\beta_1\) = slope
- \(\epsilon = error\)

Visual Explanation

Tip

How can we formalize what we are optimizing for?

Formulation

We want to find the \(\beta_0\) and \(\beta_1\) parameters that reduce the combined error.
A loss function that takes as input our parameters and whose output is our model error.
\(f(\beta_0, \beta_1) = \sum\limits_{i=1}^{n}[y_i - \hat{y}_i]^2 = \sum\limits_{i=1}^{n}\epsilon_i^2\)
Sum of the Squared Residuals (SSR/SSE). Big or small?

\[ SSR = \sum\limits_{i=1}^{n}[y_i - \hat{y}_i]^2 = [y_i - (\hat{\beta}_0 + \hat{\beta}_1 x_i)]^2 \\ = [y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i]^2 \]

Derivation

Will not be going through the derivation
Basic idea is take the partial derivaitve of the funciton with respect to the parameters and set equal to 0.
Do a bunch of algebra and you arrive at some nice equations
Full derivation is here and here

Classic Stats Result

\(\beta_1 (slope) = \frac{\sum\limits_{i=1}^{n}[(x_i-\bar{x})(y_i- \bar{y})]}{\sum\limits_{i=1}^{n} (x_i - \bar{x})^2}\)
\(\beta_0\) (intercept) - \(\bar{y} - \beta_1 \bar{x}\)

df_r = df[['bill_length_mm', 'body_mass_g']].dropna()
x = df_r.bill_length_mm
y = df_r.body_mass_g
x_bar = x.mean()
y_bar = y.mean()
print(f"Xbar: {x_bar:.1f}")
print(f"Ybar: {y_bar:.1f}")

Xbar: 43.9
Ybar: 4201.8

Computation

numerator = np.sum((x - x_bar) * (y - y_bar))
denominator = np.sum((x - x_bar)**2)
slope = numerator / denominator
intercept = y_bar - slope * x_bar
print(f"Slope: {slope:.1f}; \nIntercept: {intercept:.1f}");

Slope: 87.4; 
Intercept: 362.3

Another Classic Stats Result

\[ \begin{aligned}\hat{\beta}_1 &= \frac{\text{Cov}(x,y)}{s_x^2}\end{aligned} \]

The correlation between \(x\) and \(y\) is \(r = \frac{\text{Cov}(x,y)}{s_x s_y}\). Thus, \(\text{Cov}(x,y) = r s_xs_y\). Plugging this into above, we have

\[ \hat{\beta}_1 = \frac{\text{Cov}(x,y)}{s_x^2} = r\frac{s_ys_x}{s_x^2} = r\frac{s_y}{s_x} \]

\(\beta_0\) (intercept) - \(\bar{y} - \beta_1 \bar{x}\)

Computation

r = df_r.bill_length_mm.corr(df_r.body_mass_g)
slope = r * (df_r.body_mass_g.std() / df_r.bill_length_mm.std())
intercept = y_bar - slope * x_bar
print(f"Slope: {slope:.1f}; \nIntercept: {intercept:.1f}")

Slope: 87.4; 
Intercept: 362.3

Another Full Example

Matrix Math Result

\[ \begin{align*} A = \begin{bmatrix} x_1 & 1\\ x_2 & 1 \\ ... & ... \\ x_n & 1 \end{bmatrix} \qquad y = \begin{bmatrix} y_1 \\ y_2 \\ ... \\ y_n \end{bmatrix} \end{align*} \qquad \beta = \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} \]

\[ \hat{y_1} = x_1 \cdot \beta_0 + 1 \cdot \beta_1 \\ ... \\ \hat{y} = A \beta \]

\[ \beta = \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} = (A^TA)^{-1} A^Ty \]

Computation of Matrix Result

n = len(df_r)
print(x.shape, type(x))
x = x.values
print(x.shape,type(x))
x = np.expand_dims(x, axis=1) # convert to matrix
print(x.shape)
A = np.append(x, np.ones(shape=(n, 1)), axis=1) # add one column
print(A.shape)
y = y.values
print(x[:5, :]) # sample of matrix
# intercept = y_bar - slope * x_bar
# print(f"Slope: {slope:.1f}; \nIntercept: {intercept:.1f}")

(342,) <class 'pandas.core.series.Series'>
(342,) <class 'numpy.ndarray'>
(342, 1)
(342, 2)
[[39.1]
 [39.5]
 [40.3]
 [36.7]
 [39.3]]

Computation of Matrix Result

beta = np.linalg.inv(A.T @ A) @ A.T @ y
print(f"Slope: {beta[0]:.1f}; \nIntercept: {beta[1]:.1f}")

Slope: 87.4; 
Intercept: 362.3

Class Activity

Practice Regression