CISC482 - Lecture04
Probability
Dr. Jeremy Castagno
Class Business
Schedule
- Reading 2-2: Jan 27 @ 12PM, Friday
- Reading 2-3: Feb 1 @ 12PM, Wednesday
- HW2: Feb 1 @ Midnight, Wednesday
- Reading 3-1: Feb 3 @ 12PM, Friday
CS Faculty Candidate
- Medha Pujari is here today!
- Please attend a meet and greet at 3:15 in SBSC 112
- Extra Credit!
Probability Terms
Terms
- Random Process - action or process which results in an outcome determined by chance
- Outcome - one possible result from a random process
- Sample Space - set of all possible outcomes of a random process and denoted as \(S\)
- Event - an outcome or collection of outcomes from a sample space. Typically denoted with Capital letters: \(A,B,C\), etc.
- Probability of an event A - denoted, \(P(A)\), number of outcomes of A divided by the total number of equally likely outcomes in the sample space \(S\). How often does \(A\) occur in \(S\)
Visualizing Probability

Operations
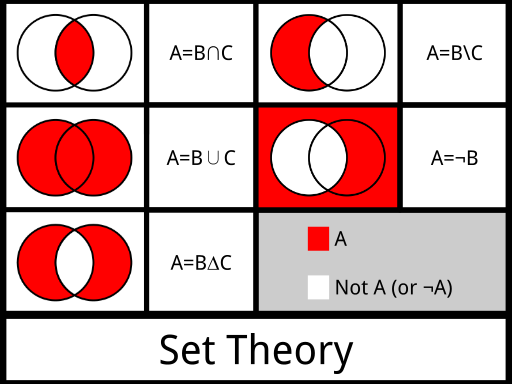
- Compliment of A - denoted not \(A\), \(A'\), \(\bar{A}\), \(A^C\), \(\neg A\)
- We will use \(A'\)
- Union of two events \(A\) and \(B\) is denoted as \(A\) or \(B\). Consists of all outcomes in \(A\) or \(B\)
- Intersection of two events \(A\) and \(B\) is denoted as \(A\) and \(B\). Consists of only outcomes in \(A\) and \(B\)
Practice
- Compliment
- Union
- Intersection
- Difference
Cheat Sheet
Probability Rules
Three Foundational Rules
- The probability of any event is non-negative, \(P(A) >= 0\)
- The probability of the sample space is \(P(S) = 1\)
- If A and be are disjoint events, \(P(A \; or \; B) = P(A) + P(B)\)
- No outcomes in common.
Three Derived Rules
- \(P(A') = 1 - P(A)\)
- \(P(A \; or \; B) = P(A) + P(B) - P(A \; and \; B)\)
- independent events: \(P(A\; and\; B) = P(A) * P(B)\)
Tip
You dont need to derive any of these, you just need to know them! Know the 6 rules
Practice
| Size | 1 | 2 | 3 | 4 | 5 | 6 | 7+ |
|---|---|---|---|---|---|---|---|
| Proportion | 0.29 | 0.35 | 0.15 | 0.12 | 0.06 | 0.02 | 0.01 |
- Find the probability of randomly selecting a household with a size of more than 1
- 0.71
- Find the probability of randomly selecting a household with a size of 1 or more than 1
- 1.0
- Find the probability of randomly selecting a household with a size of 5 or more
- 0.09
- Find the probability of randomly selecting a household with size 1 or 5 or more
- 0.38
- One household will be randomly selected from all households, and then a second household will be randomly selected from all households. Find the probability that both selected households are of size 1.
- 0.08
Conditional Probability
Prepare to be amazed
- The probability of an event occurring can also be determined under the condition of knowing another event has occurred.
- A conditioning probability is a measure of the likelihood of one event occurring, given another event occurred
The conditional probability of event \(A\) given event \(B\), denoted \(P(A|B)\)
\[ P(A|B) = \frac{P(A\; and\; B)}{P(B)} = \frac{P(A \cap B)}{P(B)} \]
Thinking Independently
- What if we have independent events, \(A,B\)
- \(P(A|B) = \frac{P(A \cap B)}{P(B)}\)
- \(P(A|B) = \frac{P(A) * P(B)}{P(B)}\)
- \(P(A|B) = P(A)\)
Conditional Example


Bayes Rule
- Sometimes you don’t have nice table with all these probabilities filled out
- You may not know \(P(A \cap B)\). Is all lost?
- No Bayes rule to the rescue!
\[ P(A | B) = \frac{P(B | A) * P(A)}{P(B)} \]
Tip
This rule is the foundation of data science and machine learning!
Example

Probability Distributions
Random Variables
- Random Variable - Defines numerical values for a random processes outcome.
- Typically denote them like: \(X,Y, Z\)
- Discrete vs Continuous - Flip of coin (1 or 0), GPA of students
- Probability Distribution - gives probability of an occurrence for a a random variable
- This distribution can be visualized! We often use histograms.
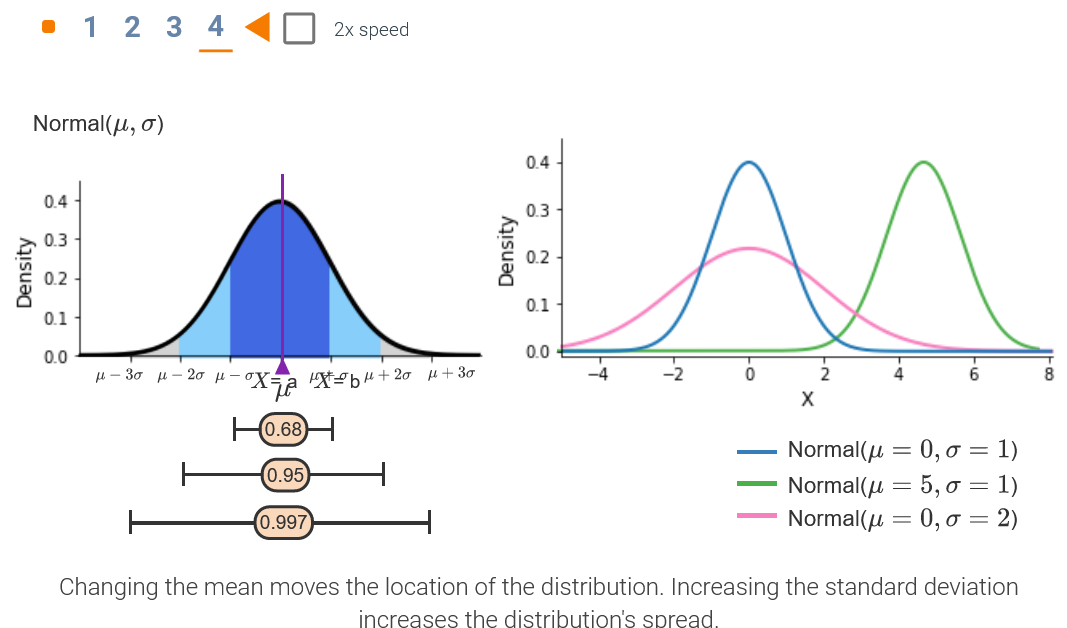
Normal Distribution
Normal Details
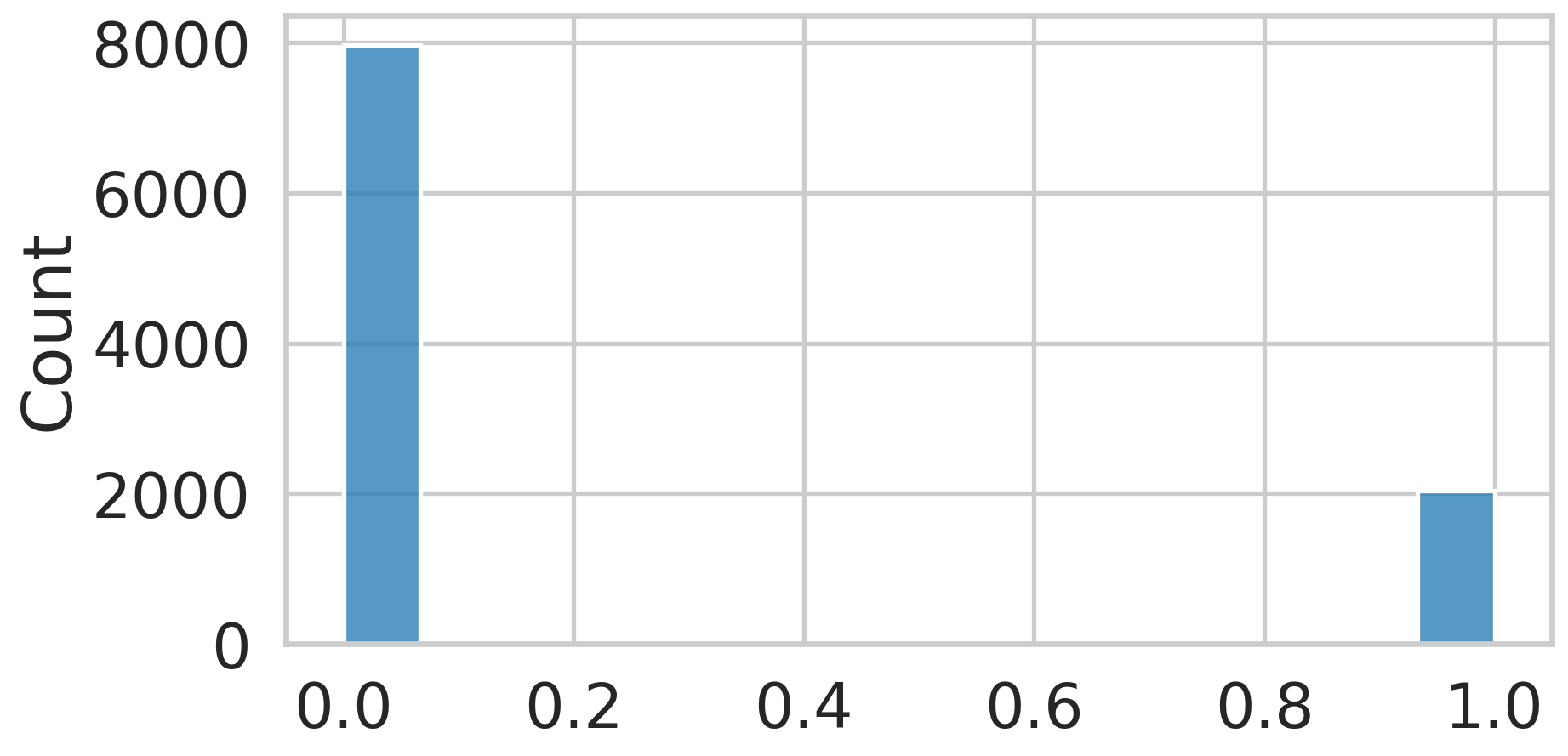
Bernoulli Distribution
- True or False, 1 or 0, Success or Failure
- \(\pi\), determines the probaility of success
- What is \(\pi\) for this bernoulli distribution
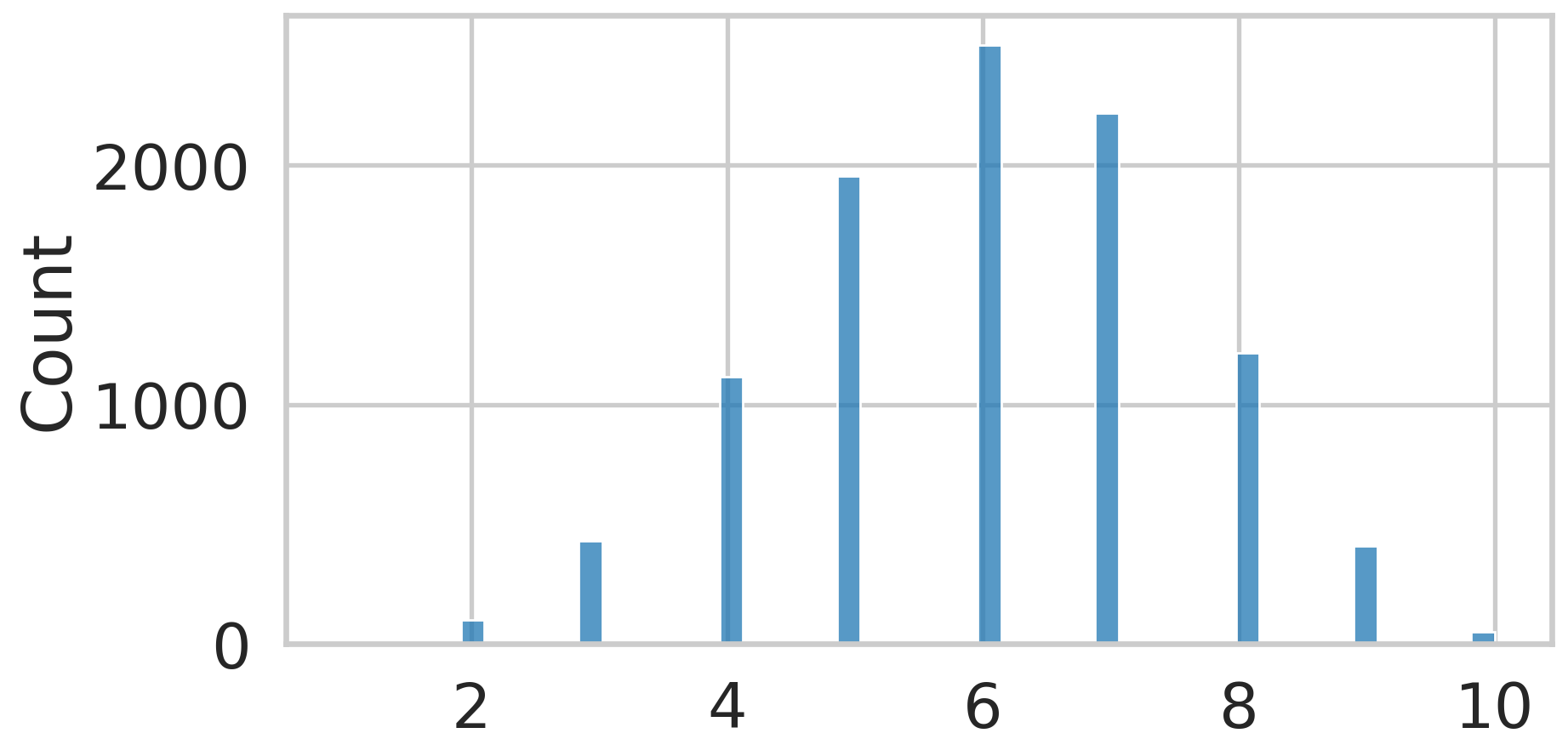
Binomial Distribution
- A random variable describing the number of “successes” from independent observations of a random process in which the probability of a success is \(\pi\) follows a binomial distribution
- Flip a coin 10 times (trials) count how many heads.
- Repeat 10,000 times to create samples
- \(n\) how many trials, \(\pi\) probability of one success
- \(\mu = n * \pi\) \(\sigma^2 = n * \pi * (1- \pi)\)
Flipping a Coin 10 Times
Note
Does this seem right?
Activity